Posted on

Is business logic too much for classical logic?

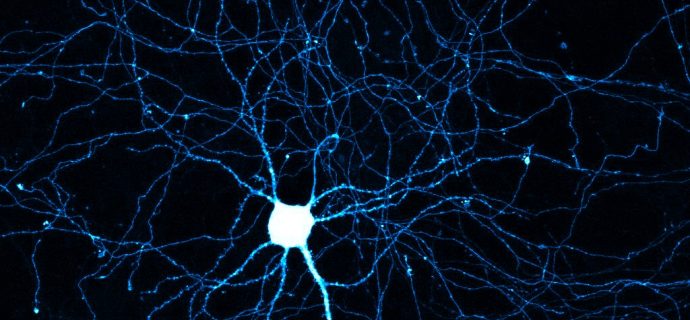
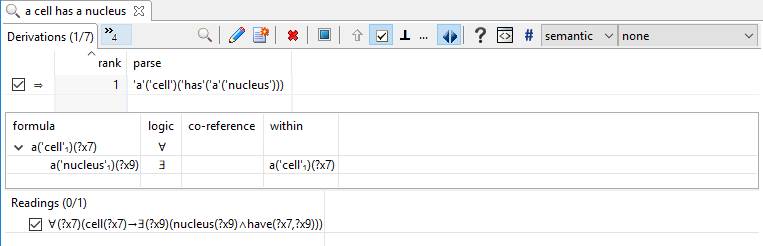
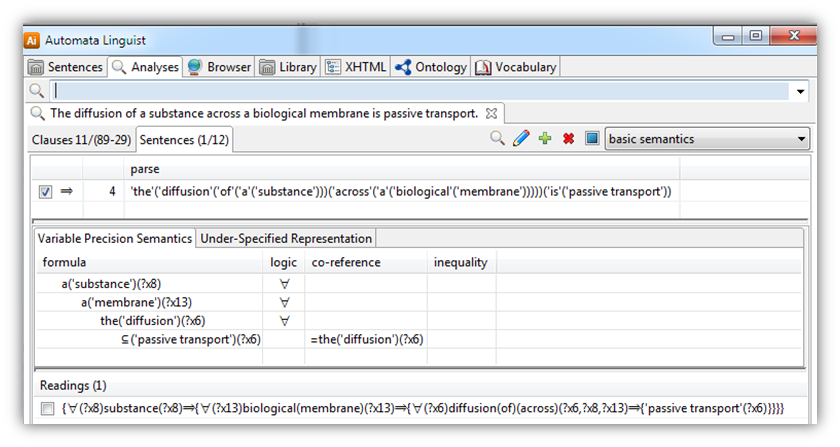
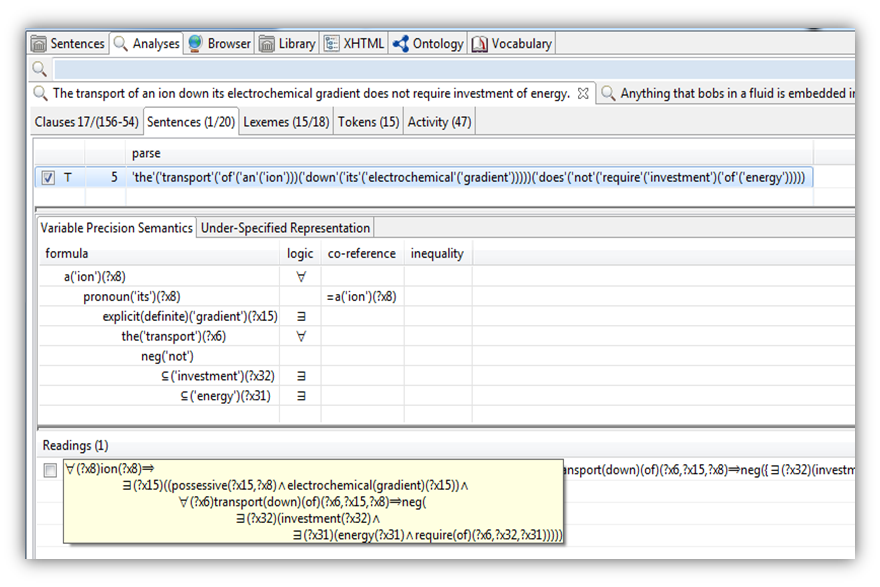
Business logic is not limited to mathematical logic, as in first-order predicate calculus.

Business logic commonly requires “aggregation” over sets of things, like summing the value of claims against a property to subtract it from the value of that property in order to determine the equity of the owner of that property.

  • The equity of the owner of a property in the property is the excess of the value of the property over the value of claims against it.

There are various ways of describing such extended forms of classical logic.  The most relevant to most enterprises is the relational algebra perspective, which is the base for relational databases and SQL.  Another is the notion of generalized quantifiers.

In either case, it is a practical matter to be able to capture such logic in a rigorous manner.  The example below shows how that can be accomplished using English, producing the following axiom in extended logic:

  • ∀(?x15)(property(?x15)→∀(?x10)(owner(of)(?x10,?x15)→∃(?x31)(value(of(?x15))(?x31)∧∑(?x44)(∀(?x49)(claim(against(?x15))(?x49)→value(of(?x49))(?x44))→∃(?x26)(excess(of(?x31))(over(?x44))(?x26)∧equity(in(?x15))(of(?x10))(?x26))))))

This logic can be realized in various ways, depending on the deployment platform, such as: Continue reading “Is business logic too much for classical logic?”

Posted on

Simply Logical English

This is not all that simple of an article, but it walks you through, from start to finish, how we get from English to logic. In particular, it shows how English sentences can be directly translated into formal logic for use with in automated reasoning with theorem provers, logic programs as simple as Prolog, and even into production rule systems.

There is a section in the middle that is a bit technical about the relationship between full logic and more limited systems (e.g., Prolog or production rule systems). You don’t have to appreciate the details, but we include them to avoid the impression of hand-waving

The examples here are trivial. You can find many and more complex examples throughout Automata’s web site.

Consider the sentence, “A cell has a nucleus.”:

Continue reading “Simply Logical English”

Posted on

Natural Intelligence

Deep natural language understanding (NLU) is different than deep learning, as is deep reasoning.  Deep learning facilities deep NLP and will facilitate deeper reasoning, but it’s deep NLP for knowledge acquisition and question answering that seems most critical for general AI.  If that’s the case, we might call such general AI, “natural intelligence”.

Deep learning on its own delivers only the most shallow reasoning and embarrasses itself due to its lack of “common sense” (or any knowledge at all, for that matter!).  DARPA, the Allen Institute, and deep learning experts have come to their senses about the limits of deep learning with regard to general AI.

General artificial intelligence requires all of it: deep natural language understanding[1], deep learning, and deep reasoning.  The deep aspects are critical but no more so than knowledge (including “common sense”).[2] Continue reading “Natural Intelligence”

Posted on

Confessions of a production rule vendor (part 1)

If you are using one of the more popular rules engines, chances are you can blame me.  I popularized the technology of forward-chaining production rules based on the Rete Algorithm.  Others have certainly contributed; my path is the one that led to open-source implementations and many commercial products, including those of IBM, Oracle, SAP, TIBCO, Red Hat, and too many others to mention (e.g., see this).

Today, I want to make clear that the future prospects for production rule technology are diminishing.  My objective here is to explain why most rule-based technologies are no good and why some are much better.  Although production rule technology is much better than most rule-based technologies, I hope to also make clear that in the age of IBM’s Watson, Google’s Brain, and the semantic web, production rule technology is inadequate.

They are not created equal.

Rules have become so pervasive in the software business that vendors of all types of software say they have them.  Consider, for example, that even Microsoft Outlook has rules!

Continue reading “Confessions of a production rule vendor (part 1)”

Posted on

Logic from the English of Science, Government, and Business

Our software is translating even long and complicated sentences from regulations to textbooks into formal logic (i.e,, not necessarily first-order logic, but more general predicate calculus).   As you can see below, we can translate this understanding into various logical formalisms including defeasible first-order logic, which we are applying in Vulcan’s Project Halo.  This includes classical first-order logic and related standards such as RIF or SBVR, as well as building or extending an ontology or description logic (e.g., OWL-DL).

We’re excited about these capabilities in various applications, such as in advancing science and education at Vulcan and formally understanding, analyzing and automating policy and regulations in enterprises.

English translated into predicate calculus

English translated into predicate calculus

a sentence understood by Automata

an unambiguously, formally understood sentence


English translated into SILK and Prolog

English translated into SILK and Prolog