This is not all that simple of an article, but it walks you through, from start to finish, how we get from English to logic. In particular, it shows how English sentences can be directly translated into formal logic for use with in automated reasoning with theorem provers, logic programs as simple as Prolog, and even into production rule systems.
There is a section in the middle that is a bit technical about the relationship between full logic and more limited systems (e.g., Prolog or production rule systems). You don’t have to appreciate the details, but we include them to avoid the impression of hand-waving
The examples here are trivial. You can find many and more complex examples throughout Automata’s web site.
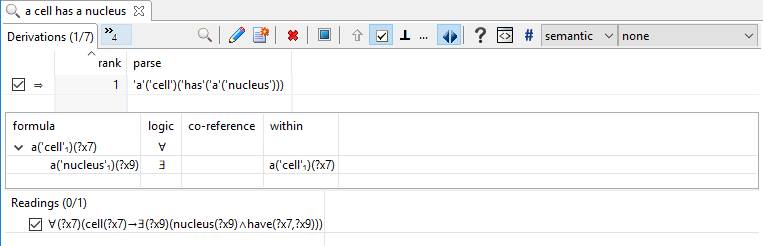
Consider the sentence, “A cell has a nucleus.”:
The axiom of first-order predicate calculus at the bottom shows a universal quantifier of the variable “?x7”.
- This can be read as “for every cell”.
The axiom also shows an existential quantifier of variable “?x9” which applies to a conjunction of 2 “atomic” formulas.
- This can be read as “there exists a nucleus that the cell has”.
This is fine logic. One could equally quibble about the lack of precise semantics of “have” or argue that the lack of precision is appropriate.[1]
So, rather than get pedantic, let’s discuss the utility of this (and similar) representations…
As discussed in this background on logic, formal ontology expresses knowledge as sentences of logic (rather than sentences of English). The types of logic vary from predicate calculus to descriptions logics (e.g., the web ontology language) to Horn clauses (e.g., Prolog). Each of these sentences is called an “axiom”. When some knowledge is expressed in such axioms we call it “axiomatic knowledge”. he important thing about axiomatic knowledge is that it is less ambiguous than knowledge expressed in English and more amenable to automated reasoning technology.
The following axiom is first-order logic:
- ∀(?x7)(cell(?x7)→∃(?x9)(nucleus(?x9)∧have(?x7,?x9)))
Theorem provers perform classical reasoning with first-order logic axioms. Classical logical reasoning with theorem provers is fraught with challenges and limitations, however. If the problem they are asked is not decidable, they can take forever to give no answer. Furthermore, classical theorem provers will errantly conclude anything or everything is true or false given inconsistent knowledge. Unfortunately, determining whether a set of first-order axioms is consistent is undecidable!
More practical logic programming systems provide means of handling inconsistent knowledge and bounded rationality. Here we will demonstrate using Flora, an open-source, higher-order, defeasible logic programming system. See the above-referenced page for details.
A Prolog query shows the axiom above as it is represented in Flora:
- ?reading = ‘∀'(\##7)(‘→'(cell(\##7),’∃'(\##9)(‘∧'(nucleus(\##9),have(\##7,\##9)))))
Note that the “?x” shown on screen has been changed to “\##” in Flora.
- Such readings can be targeted to various theorem provers by converting them to conjunctive or clause normal form (CNF).
- Such readings can also be targeted to logic programming systems and rule-based systems, as discussed below.
Doing is a multi-step process involving:
- reducing the scope of negation to atomic formulas (i.e., conversion to negation normal form, NNF)
- eliminating quantifiers (i.e., converting to skolem normal form, SNF)
- making universal quantification implicit, and
- replacing existentially quantified variables with “skolem functions”
- extracting a conjunction of clauses by conversion to conjunctive normal form (CNF)
- a clause is a conjunction of literals, each which is a possibly negated atomic formula[2]
Applying these steps to the reading above results in the following intermediate results:
- ?nnf = ‘∀'(\##7)(‘∨'([‘¬'(cell(\##7)), ‘∃'(\##9)(‘∧'([nucleus(\##9), have(\##7,\##9)]))]))
- ?snf = ‘∨'([‘¬'(cell(\##7)), ‘∧'([nucleus(skolem(\##9,\##7)), have(\##7,skolem(\##9,\##7))])])
- ?cnf = ‘∧'([‘∨'([‘¬'(cell(\##7)), nucleus(skolem(\##9,\##7))]), ‘∨'([‘¬'(cell(\##7)), have(\##7,skolem(\##9,\##7))])])
Note that the variable for “?x9” (designated “\##9”) has been replaced by a function of variable “?x7” (designated \##7).
- skolem(?x9,?x7) is a “skolem function” [3] which binds variable “?x9” to the nucleus of cell ?x7
All that really matters here is that a collection of logical sentences (i.e., axiomatic knowledge) is converted into a larger collection of clauses to be feed into a theorem prover or translated into a logic programming or production rule system.
- Theorem provers typically take CNF (i.e., a set of clauses) as their input.
- Logic programming languages (e.g., Prolog) take Horn clauses as their input.
The following shows the result of another query showing the clauses of the CNF above translated into Flora:
- ?rule = \neg cell(\##7) :- \neg nucleus(skolem(\##9,\##7))
- ?rule = nucleus(skolem(\##9,\##7)) :- cell(\##7)
- ?rule = \neg cell(\##7) :- \neg have(\##7,skolem(\##9,\##7))
- ?rule = have(\##7,skolem(\##9,\##7)) :- cell(\##7)
We simply write these out to a file substituting variables and changing the skolem functions a little, to yield:
- \neg cell(?x7) :- \neg nucleus(f9(?x7)).
- nucleus(f9(?x7)) :- cell(?x7).
- \neg cell(?x7) :- \neg have(?x7,f9(?x7)).
- have(?x7,f9(x7)) :- cell(?x7).
The “’\neg” in these rules can be read as “it is not the case” or “it is false that”. The 1st and 2nd of these rules are the inverse of each other (i.e., they are contrapositives[4]), as are the 3rd and 4th. Making contrapositives explicit helps logic programs realize more of the power of theorem proving. Doing so requires functionality lacking in standard Prolog, which is provided in Flora and XSB.
The 1st and 3rd rules are typically omitted from non-logical systems. The first says, in effect, if a certain function of ?x7 is not a nucleus then ?x7 cannot be a cell. The third says, essentially, if ?x7 does not have the same certain function of ?x7 then ?x7 cannot be a cell.
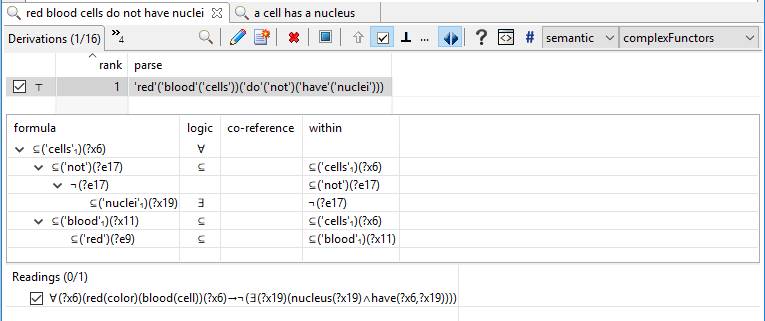
To understand more about why these rules may be retained in a logical system, consider the following:
In NNF, this reads as follows:
- ?sentence = ‘∀'(\##6)(‘∨'([‘¬'(red(color)(blood(cell))(\##6)), ‘∀'(\##19)(‘∨'([‘¬'(nucleus(\##19)), ‘¬'(have(\##6,\##19))]))]))
From which the following Flora rules are derived:
- \neg red(color)(blood(cell))(?x6) :- (nucleus(?x19), have(?x6,?x19))
- \neg nucleus(?x19) :- (red(color)(blood(cell))(?x6), have(?x6,?x19))
- \neg have(?x6,?x19) :- (red(color)(blood(cell))(?x6), nucleus(?x19))
Note that the two sentences contradict and that the resulting rules will infer that the result of the skolem function (f9) is both a nucleus and not a nucleus. Such logical contradictions “break” theorem provers. They do not break the well-founded semantics or defeasible logic systems, such as XSB and Flora, however. The point here is not to get into all that (we’ll save that for other posts), but to indicate that there is so utility (even power) to be obtained by retaining the contrapositives.[5]
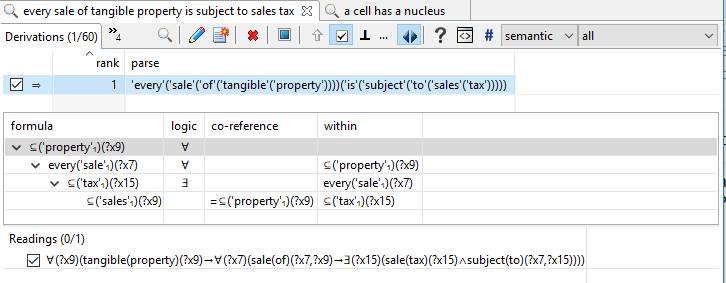
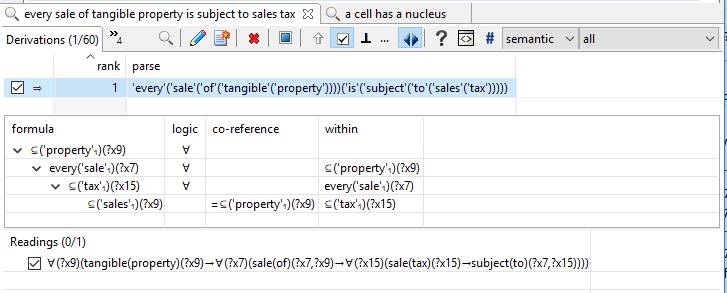
Here is a final example (for this article) of how this looks in a more business-oriented setting:
This results in the following Flora rules:
- \neg tangible(property)(?x9) :- (sale(of)(?x7,?x9), \neg sale(tax)(f15(?x7,?x9)))
- \neg sale(of)(?x7,?x9) :- (tangible(property)(?x9), \neg sale(tax)(f15(?x7,?x9)))
- sale(tax)(f15(?x7,?x9)) :- (tangible(property)(?x9), sale(of)(?x7,?x9))
- \neg tangible(property)(?x9) :- (sale(of)(?x7,?x9), \neg subject(to)(?x7,f15(?x7,?x9)))
- \neg sale(of)(?x7,?x9) :- (tangible(property)(?x9), \neg subject(to)(?x7,f15(?x7,?x9)))
- subject(to)(?x7,f15(?x7,?x9)) :- (tangible(property)(?x9), sale(of)(?x7,?x9))
Where f15(?x,?y) is a function representing a tax that a sale ?x of property ?y is subject to.
People who are more comfortable with the latent limitations of business rules systems, might need time to understand the foregoing completely. To make this even more concrete, such as assuming the only tax under consideration is California sales tax, we would have:
For which the rules are:
- \neg sale(tax)(?x15) :- (tangible(property)(?x9), (sale(of)(?x7,?x9), \neg subject(to)(?x7,?x15)))
- \neg tangible(property)(?x9) :- (sale(of)(?x7,?x9), (sale(tax)(?x15), \neg subject(to)(?x7,?x15)))
- \neg sale(of)(?x7,?x9) :- (tangible(property)(?x9), (sale(tax)(?x15), \neg subject(to)(?x7,?x15)))
- subject(to)(?x7,?x15) :- (tangible(property)(?x9), (sale(of)(?x7,?x9), sale(tax)(?x15)))
And for those who are using current business rule engines, this would boil down to only the last of these lines:
- subject(to)(?x7,?x15) :- (tangible(property)(?x9), (sale(of)(?x7,?x9), sale(tax)(?x15)))
Which can also, of course, be generated for a forward-chaining Rete Algorithm, such as in CLIPS, JESS, Drools (Red Hat Decision Manager), JRules (IBM Operational Decision Manager), as in the following syntax:
(defrule “every sale of tangible property is subject to sales tax”
(sale_of ?x7 ?x9)
(tangible_property ?x9)
(sales_tax ?x15)
==>
(assert (subject_to ?x7 ?x15))
)
And, of course, there is more to say about aligning any such representations with implementation details via an intermediate ontology (which also manages the domain vocabulary). But for now, the point has been made:
It’s easy to translate English into powerful logic for policy automation, decision management, compliance, and question answering.
[1] e.g., does “has” here mean “owns”, “contains”, “part of”, etc.
[2] more on the terminology of logic and logic programming is here
[3] https://www.encyclopediaofmath.org/index.php/Skolem_function
[4] https://en.wikipedia.org/wiki/Contraposition
[5] This type of robustness is unheard of in production systems but is important in commercial progress, such as in recognizing the need to raise an (as yet) unhandled exception. Using the capabilities of defeasible logic, such exceptions can be explicitly handled, such as in accordance with policies.
2 Replies to “Simply Logical English”
Comments are closed.