Posted on

A pedagogical model by any other name

Educational technology for personalized or adaptive learning is based on various types of pedagogical models.

Google provides the following info-box and link concerning pedagogical models:

Many companies have different names for their models, including:

  1. Knewton: Knowledge Graph
    (partially described in How do Knewton recommendations work in Pearson MyLab)
  2. Kahn Academy: Knowledge Map
  3. Declara: Cognitive Graph

The term “knowledge graph” is particularly common, including Google’s (link).

There are some serious problems with these names and some varying limitations in their pedagogical efficacy.  There is nothing cognitive about Declara’s graph, for example.  Like the others it may organize “concepts” (i.e., nodes) by certain relationships (i.e., links) that pertain to learning, but none of these graphs purports to represent knowledge other than superficially for limited purposes.

  • Each of Google’s, Knewton’s, and Declara’s graphs are far from sufficient to represent the knowledge and cognitive skills expected of a masterful student.
  • Each of them is also far from sufficient to represent the knowledge of learning objectives and instructional techniques expected of a proficient instructor.

Nonetheless, such graphs are critical to active e-learning technology, even if they fall short of our ambitious hope to dramatically improve learning and learning outcomes.

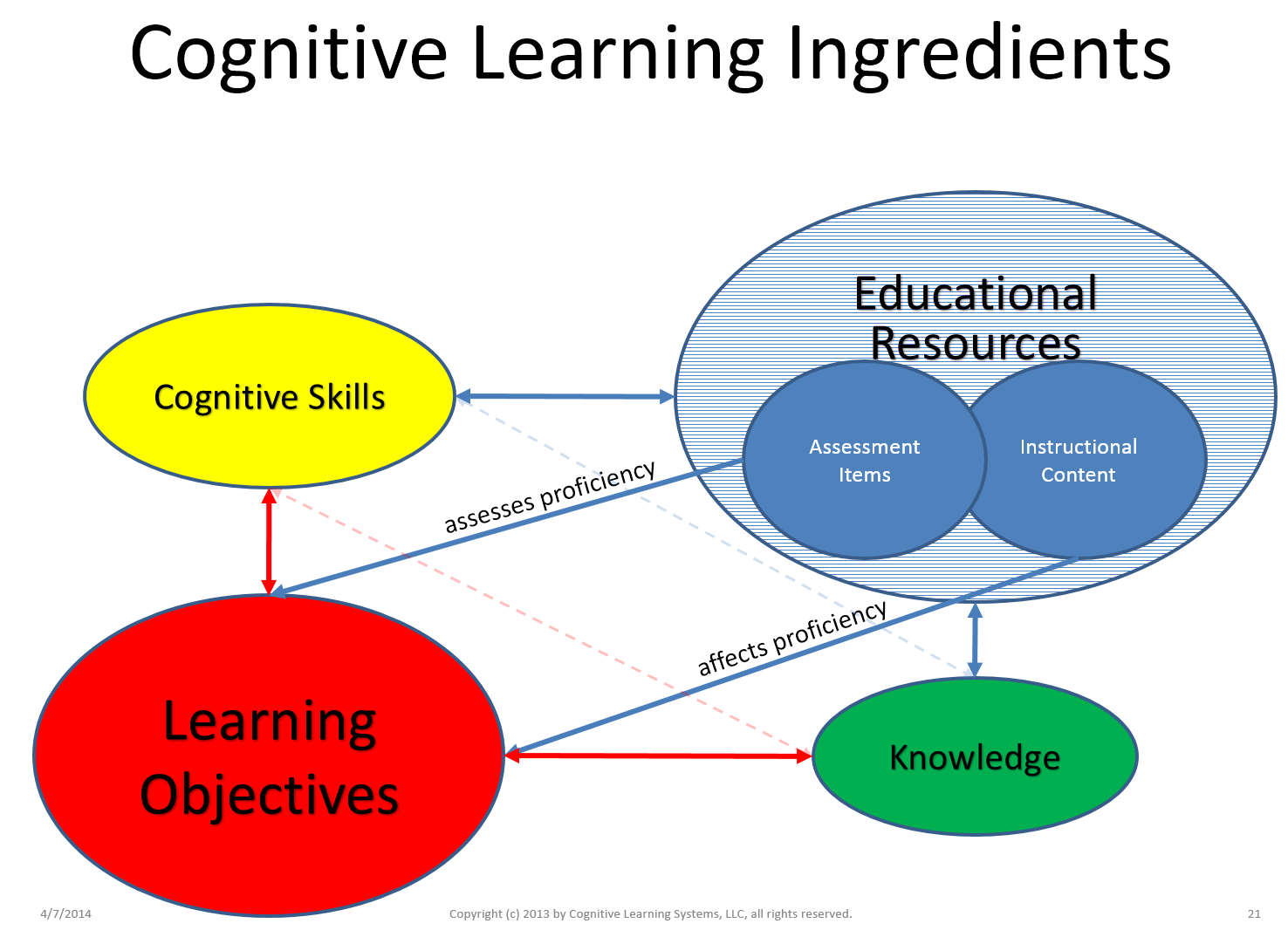
The most critical ingredients of these so-called “knowledge” or “cognitive” graphs include the following:

  1. learning objectives
  2. educational resources, including instructional and formative or summative assessment items
  3. relationships between educational resources and learning objectives (i.e., what they instruct and/or assess)
  4. relationships between learning objectives (e.g., dependencies such as prerequisites)

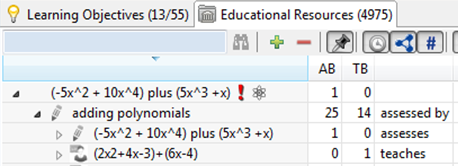
The following user interface supports curation of the alignment of educational resources and learning objectives, for example:

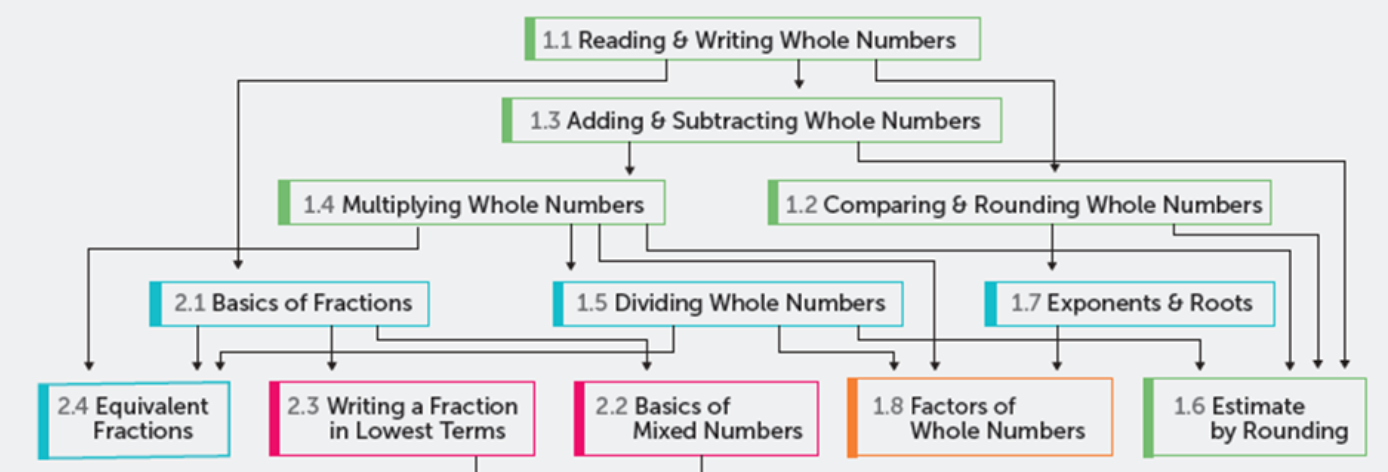
And the following supports curation of the dependencies between learning objectives (as in a prerequisite graph):

Here is a presentation of similar dependencies from Kahn Academy:

And here is a depiction of such dependencies in Pearson’s use of Knewton within MyLab (cited above):

Of course there is much more that belongs in a pedagogical model, but let’s look at the fundamentals and their limitations before diving too deeply.

Prerequisite Graphs

The link on Knewton recommendations cited above includes a graphic showing some of the learning objectives and their dependencies concerning arithmetic.  The labels of these learning objectives include:

  • reading & writing whole numbers
  • adding & subtracting whole numbers
  • multiplying whole numbers
  • comparing & rounding whole numbers
  • dividing whole numbers

And more:

  • basics of fractions
  • exponents & roots
  • basics of mixed numbers
  • factors of whole numbers

But:

  • There is nothing in the “knowledge graph” that represents the semantics (i.e., meaning) of “number”, “fraction”, “exponent”, or “root”.
  • There is nothing in the “knowledge graph” that represents what distinguishes whole from mixed numbers (or even that fractions are numbers).
  • There is nothing in the “knowledge graph” that represents what it means to “read”, “write”, “multiply”, “compare”, “round”, or “divide”.

Graphs, Ontology, Logic, and Knowledge

Because systems with knowledge or cognitive graphs lack such representation, they suffer from several problems, including the following, which are of immediate concern:

  1. dependencies between learning objectives must be explicitly established by people, thereby increasing the time, effort, and cost of developing active learning solutions, or
  2. learning objectives that are not explicitly dependent may become dependent as evidence indicates, which requires exponentially increasing data as the number of learning objectives increases, thereby offering low initial and asymptotic efficacy versus more intelligent and knowledge-based approaches

For example, more advanced semantic technology standards (e.g., OWL and/or SBVR or defeasible modal logic) can represent that digits are integers are numbers and an integer divided by another is a fraction.  Consequently, a knowledge-based system can infer that learning objectives involving fractions depend on some learning objectives involving integers.  Such deductions can inform machine learning such that better dependencies are induced (initially and asymptotically) and can increase the return on investment of human intelligence in a cognitive computing approach to pedagogical modeling.

As another example, consider that adaptive educational technology either knows or do not know that multiplication of one integer by another is equivalent to computing the sum of one the other number of times.  Similarly, they either know or they do not know how multiplication and division are related.  How effectively can the improve learning if they do not know?  How much more work is required to get such systems to achieve acceptable efficacy without such knowledge?  Would you want your child instructed by someone who was incapable of understanding and applying such knowledge?

Semantics of Concepts, Cognitive Skills, and Learning Objectives

Consider again the labels of the nodes in Knewton/Pearson’s prerequisite graph listed above.  Notice that:

  • the first group of labels are all sentences while the second group are all noun phrases
  • the first group (of sentences) are cognitive skills more than they are learning objectives
    • i.e., they don’t specify a degree of proficiency, although one may be implicit with regard to the educational resources aligned with those sentences
  • the second group (of noun phrases) refer to concepts (or, implicitly, sentences that begin with “understanding”)
  • the second group (of noun phrases) that begin with “basics” are unclear learning objectives or references to concepts

For adaptive educational technology that does not “know” what these labels mean nor anything about the meanings of the words that occur in them, the issues noted above may not seem important but they clearly limit the utility and efficacy of such graphs.

Taking a cognitive computing approach, human intelligence helps artificial intelligence understand these sentences and phrases deeply and precisely.  A cognitive computing approach also results in artificial intelligence that deeply and precisely understands many additional sentences of knowledge that don’ fit into such graphs.

For example, the system comes to know that reading and writing whole numbers is a conjunction of finer grained learning objectives and that, in general, reading is a prerequisite to writing.  It comes to know that whole numbers are non-negative integers which are typically positive.  It comes to know that subtraction is the inverse of addition (which implies some dependency relationship between addition and subtraction).  In order to understand exponents, the system is told and learns about raising numbers to powers and about what it means to square a number.  The system is told and learns about roots how they relate to exponents and powers, including how square roots relate to squaring numbers.  The system is told that a mixed number is an integer and proper fraction corresponding to an improper fraction.

Adaptive educational technology either understands such things or it does not.  If it does not, human beings will have to work much harder to achieve a system with a given level of efficacy and subsequent machine learning will take a longer time to reach a lower asymptote of efficacy.

Posted on

A good example of the need for better assessment

The Andes Physics Tutor [1,2] is a nice piece of work.  Looking at the data from the Spring 2010 physics course at the US Naval Academy [3] there are obvious challenges facing the current generation of adaptive education vendors.

Most of the modeling going on today is limited to questions where a learner gets the answer right or wrong with nothing in between.  Most assessment systems use such simple “dichotomous” models based on item response theory (IRT).  IRT models range in sophistication based on the number of “logistic parameters” that the models use to describe assessment items.  IRT models also come in many variations that address graded responses (e.g., Likert scales [4]) or partial credit and onto multi-dimensional and/or multi-level/hierarchical and/or longitudinal models.  I am not aware of any model that addresses the richness of pedagogical data available from the physics tutor, however.

Having spent too long working through too much of the research literature in the area, a summary path through all this may be helpful…  There are 1, 2, and 3 parameter logistic IRT models that characterize assessment items in terms of their difficulty, discrimination, and guess-ability. These are easiest to understand initially in the context of an assessment item that assesses a single cognitive skill by scoring a learner’s performance as passing or failing on the item.   Wikipedia does a good job of illustrating how these three numbers describe the cumulative distribution function of the probability that a learner will pass as his or her skill increases [5].   A 1 parameter logistic (1PL) model describes an assessment item only in terms of a threshold of skill at which half the population falls on either side.  The 2PL IRT model also considers the steepness of the curve.  The steeper it is the more precisely the assessment item discriminates between above and below average levels of skill.  And the 3PL model takes into consideration the odds that the a passing result is a matter of luck, such as in guessing the right answer from a multiple choice question.

In the worlds of standardized testing and educational technology, especially with regard to personalized learning (as in adaptive assessment, curriculum sequencing, and intelligent tutoring), multiple choice and fill-in-the-blank questions dominate because grading can be automated.  It is somewhat obvious then that 3PL IRT is the appropriate model for standardized testing (which is all multiple choice) and a large fraction of personalized learning technology.  Fill-in-the-blank questions are sometimes less vulnerable to guessing, in which case 2PL may suffice.  You may be surprised to learn, however, that even though 3PL is strongly indicated, its use is not pervasive because estimating the parameters of a 3PL model is mathematically and algorithmically sophisticated as well as computationally demanding.  Nonetheless, algorithmic advances in Bayesian inference have matured over the last decade such that 3PL should become much more pervasive in the next few years.  (To their credit, for example, Knewton appears to use such techniques [6].)

It gets worse, though.  Even if an ed-tech vendor is sophisticated enough to employ 3PL IRT, they are far less likely to model assessment items that involve multiple or hierarchical skills and assessments other than right or wrong. And there’s more beyond these complications, but let’s pause to consider two of these for a moment.  In solving a word problem, such as in physics or math, for example, a learner needs linguistic skills to read and comprehend the problem before going on to formulate and solve the problem.  These are different skills.  They could be modeled coarsely, such as a skill for reading comprehension, a skill for formulating equations, and a skill for solving equations,  but conflating these skills into what ITR folks sometimes call a single latent trait is behind the state of the art.

Today, multi-dimensional IRT is hot given recent advances in Bayesian methods.  Having said that, it’s worth noting that multiple skills have been on experts’ minds for a long time (e.g., [7]) and have been prevalent in higher-end educational technology, such as intelligent tutoring systems (aka, cognitive tutors), for years.  These issues are prevalent in almost all the educational data available at PLSC’s DataShop [3].  Unfortunately, the need to associate multiple skills with assessment items exacerbates a primary obstacle to broader deployment of better personalized learning solutions: pedagogical modeling.  One key aspect of a pedagogical model is the relationship between assessment items and the cognitive skills they require (and assess).  Given such information, multi-dimensional IRT can be employed, but even articulating a single learning objective per assessment item and normalizing those learning objectives over thousands of assessment items is a major component of the cost of developing curriculum sequencing solutions.  (We’ll be announcing progress on this problem “soon”.)

In addition to multi-dimensional IRT, which promises more cognitive tutors, there are other aspects of modeling assessment, such as in hierarchical or multi-level IRT.   Although the terms hierarchical and multi-level are sometimes used interchangeably with respect to models of assessment, we are more comfortable with the former being with respect to skills and the latter with regard to items.  A hierarchical model is similar to a multi-dimensional model in that an item involves multiple skills but most typically where those skills have some taxonomic relationship.  A multi-level model allows for shared structure or focus between assessment items, including multiple questions concerning a common passage  or scenario, as well as drill-down items.  All of the issues discussed in this paragraph are prevalent in the Andes Physics Tutor data.  Many other data models available at PLSC’s Datashop also involve hierarchically organization of multiple skills (aka, “knowledge components”).

And we have yet to address other critical aspects of a robust model of assessment!  For example, we have not considered how the time taken to perform an assessment reflects on a learner’s skil nor graded responses or grades other than pass/fail (i.e., polytomous vs. dichotomous models).  The former is available in the data (along with multiple attempts, hints, and explanations that we have not touched on).  The latter  remains largely unaddressed despite being technically straightforward (albeit somewhat sophisticated).  All of these are important, so put them on your assessment or pedagogical modeling and personalized learning checklist and stay posted!

[1] http://www.andestutor.org/

[2] Vanlehn, Kurt, et al. “The Andes physics tutoring system: Lessons learned.” International Journal of Artificial Intelligence in Education 15.3 (2005): 147-204.

[3] available on-line at the Pittsburgh Learning Sciences Collaboration (PLSC) Datashop

[4] Likert scales & items at Wikipedia

[5] the item response function of ITR at Wikipedia

[6] see the references to Monte Carlo Markov Chain estimation of ITR models in this post from Knewton’s tech blog

[7] Kelderman, Henk, and Carl PM Rijkes. “Loglinear multidimensional IRT models for polytomously scored items.” Psychometrika 59.2 (1994): 149-176.

Posted on

Personalized e-Learning Styles

Although a bit of a stretch, this post was inspired by the following blog post, which talks about the Facebook API in terms of learning styles. If you’re interested in such things, you are probably also aware of learning record stores and things like the Tin Can API.  You need these things if you’re supporting e-learning across devices, for example…

Really, though, I was looking for information like the following nice rendering from Andrew Chua:

There’s a lot of hype in e-learning about what it means to “personalize” learning.  You hear people say that their engagements (or recommendations for same) take into account individuals’ learning styles.  Well…

Continue reading “Personalized e-Learning Styles”

Posted on

Authoring questions for education and assessment

Thesis: the overwhelming investment in educational technology will have its highest economic and social impact in technology that directly increases the rate of learning and the amount learned, not in technology that merely provides electronic access to abundant educational resources or on-line courses.  More emphasis is needed on the cognitive skills and knowledge required to achieve learning objectives and how to assess them.

Continue reading “Authoring questions for education and assessment”

Posted on

Cognitive modeling of assessment items

Look for a forthcoming post on the broader subject of personalized e-learning.  In the meantime, here’s a tip on writing good multiple choice questions:

  • target wrong answers to diagnose misconceptions.

Better approaches to adaptive education model the learning objectives that are assessed by questions such as the following from the American Academy for the Advancement of Science which goes the extra mile to also model the misconceptions underlying incorrect answers:

Posted on

Electronically enhanced learning

We are working on educational technology.  That is, technology to assist in education.  More specifically, we are developing software that helps people learn.  There are many types of such software.  We are most immediately focused on two such types.

  1. adaptive educational technology for personalized learning
  2. cognitive tutors

The term “adaptive” with regard to educational technology has various interpretations.  Educational technology that adapts to individuals in any of various ways is the most common interpretation of adaptive educational technology.  This interpretation is a form of personalized learning.  Personalized learning is often considered a more general term which includes human tutors who adapt how they engage with and educate learners.  In the context of educational technology, these senses of adaptive and personalized learning are synonymous. Continue reading “Electronically enhanced learning”