Recently, we “read” ten thousand recipes or so from a cooking web site. The purpose of doing so was to produce a formal representation of those recipes for use in temporal reasoning by a robot.
Our task was to produce ontology by reading the recipes subject to conflicting goals. On the one hand, the ontology was to be accurate so that the robot could reason, plan, and answer questions robustly. On the other hand, the ontology was to be produced automatically (with minimal human effort).[1]
In order to minimize human effort while still obtaining deep parses from which we produce ontology, we used more techniques from statistical natural language processing than we typically do in knowledge acquisition for deep QA, compliance, or policy automation. (Consider that NLP typically achieves less than 90% syntactic accuracy while such work demands near 100% semantic accuracy.)[2]
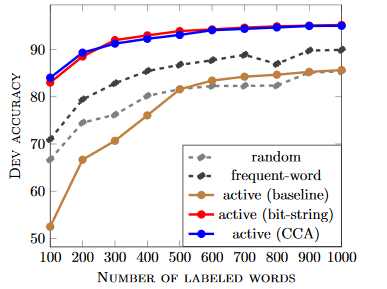
In the effort, we refined some prior work on representing words as vectors and semi-supervised learning. In particular, we adapted semi-supervised, active learning similar to Stratos & Collins 2015 using enhancements to the canonical correlation analysis (CCA) of Dhillon et al 2015 to obtain accurate part of speech tagging, as conveyed in the following graphic from Stratos & Collins: