This provides some background relating to some work we did on part of speech tagging for a modest, domain-specific corpus. The path is from Hsu et al 2012, which discusses spectral methods based on singular value decomposition (SVD) as a better method for learning hidden Markov models (HMM) and the use of word vectors instead of clustering to improve aspects of NLP, such as part of speech tagging.
The use of vector representations of words for machine learning in natural language is not all that new. A quarter century ago, Brown et al 1992 introduced hierarchical agglomerative clustering of words based on mutual information and the use of those clusters within hidden Markov language models. One notable difference versus today’s word vectors is that paths through the hierarchy of clusters to words at the leaves correspond to vectors of bits (i.e., Boolean features) rather than real-valued features.
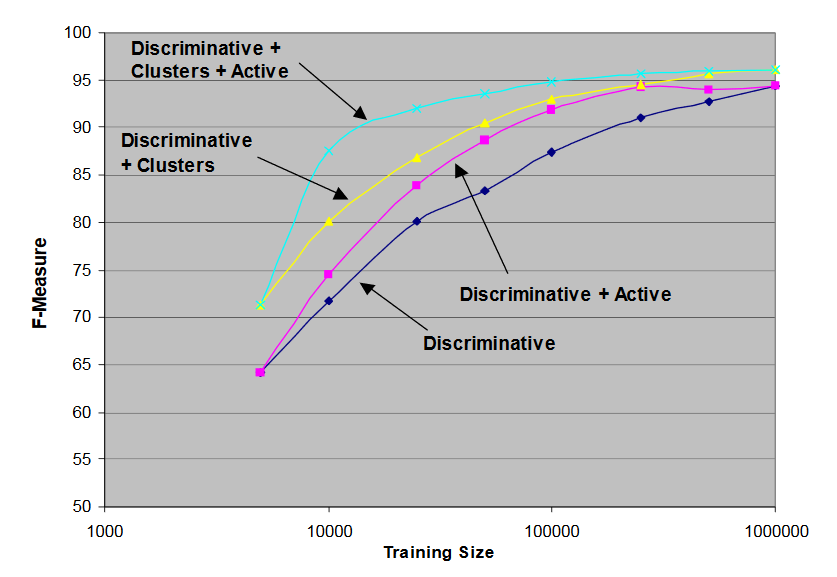
Miller et al 2004 used Brown’s approach with active learning to address needs similar to those of our client, as indicated by the following from their paper:
At a recent meeting, we presented name-tagging technology to a potential user. The technology had performed well in formal evaluations, had been applied successfully by several research groups, and required only annotated training examples to configure for new name classes. Nevertheless, it did not meet the user’s needs.
To achieve reasonable performance, the HMM-based technology we presented required roughly 150,000 words of annotated examples, and over a million words to achieve peak accuracy. Given a typical annotation rate of 5,000 words per hour, we estimated that setting up a name finder for a new problem would take four person-days of annotation work – a period we considered reasonable. However, this user’s problems were too dynamic for that much setup time. To be useful, the system would have to be trainable in minutes or hours, not days or weeks.
The paper demonstrates a remarkable improvement even though the approaches were limited to pairs of adjacent words (i.e., bigrams). Generally, the longer the n-grams used, the better HMM approaches perform. For example, the trigrams (i.e., sequences of 3 words) that occur in text subsume the bigrams in the text but not vice-versa, so trigrams provide more information from which to learn.
There is a lot of literature on distributed representation of words. Typically, such representations are points in a high-dimensional space in which “similar” words are “close”. Such representations include Word2Vec and GloVe. The former vectors were obtained using neural networks while the latter were derived from co-occurrence matrices.[1]
Stratos et al 2014 demonstrated a more efficient approach (than Brown clustering) which yields similar results using hierarchical agglomerative clustering of real-valued vectors produced by canonical correlation analysis (CCA).
More recently, Stratos & Collins 2015 dropped the clustering and used the “eigenvectors” produced by CCA to achieve excellent results. In that work, they also employed active learning, as in Miller et al. The reduction in tagging effort required to achieve excellent performance is stunning.
Having recently implemented a vision system for 3D body tracking, I enjoyed contemplating the following statement from Hsu et al 2012, in particular:
The subspace identification methods, used in control theory, use spectral approaches to discover the relationship between hidden states and the observations. In this literature, the relationship is discovered for linear dynamical systems such as Kalman filters. The basic idea is that the relationship between observations and hidden states can often be discovered by spectral/SVD methods correlating the past and future observations (in particular, such methods often do a CCA between the past and future observations).
The analogy between Kalman filtering and HMMs is a nice one!
[1] from which GloVe derives the co-occurrence probabilities which are the basis for the algorithm
One Reply to “Of Kalman Filters and Hidden Markov Models”
Comments are closed.