I have previously written about the lack of a common upper ontology in the semantic web and commercial software markets (e.g., business rules). For example, the lack of understanding of time limits the intelligence and ease of use of software in business process management (BPM) and complex event processing (CEP). The lack of understanding of money limits the intelligence and utility of business rules management systems (BRMS) in financial services and the capital markets. And, more fundamentally, understanding time and money (among other things, such as location, which includes distance) requires a core understanding of amounts.
- Understanding events and processes takes time
- Oracle should teach Siebel CRM about location and money
- Ontology of time in progress – amounts needed
The core principle here is that software needs to have a common core of understanding that makes sense to most people and across almost every application. These are the concepts of Pareto’s 80/20 Principle. A concept like building could easily be out, but concepts like money and time (and whatever it takes to really understand money and time) are in. Location, including distance, is in. Luminousity could be out, but probably not if color is in. Charge and current could be out, but not if electricity or magnetism is in. The cutoff is less scientific than practical, but what is in has to be deeply consistent and completely rational (i.e., logically rigorous).[2]
Angle is in
It took working with a team that is getting software to pass AP tests in physics, chemistry, and other areas (e.g., biology and economics) for me to realize that the physicists and chemists who defined the the International System of Units overlooked something fundamental not only to math and physics, but to our integration of language with visual perception.
It turns out that understanding angles can be just as important – and is just as primitive – as understanding distance. Consider longitude and latitude, for example. And if you’re trying to get a computer to get college credit by passing the advanced placement test for Physics , then you need to understand angular momentum.
Surprisingly, distance is among the SI units, but angle is not![1]
Getting computers to understand angles involves circles and fractions, which bring a few other concepts into our upper ontology, such as diameter, circumference, arcs, and denominators and numerators. Curiously, angles are primitive and yet they are intrinsically fractions of circles.
A piece of a pie could be an eighth or a sixth of the whole pie. The angle of either such piece would be 30 or 45 degrees, since there are 360 degrees in a circle (assuming the pie is round).
What is an angle?
Here’s what Wikipedia has to say on the matter:
In geometry and trigonometry, an angle (in full, plane angle) is the figure formed by two rays sharing a common endpoint, called the vertex of the angle. The magnitude of the angle is the “amount of rotation” that separates the two rays, and can be measured by considering the length of circular arc swept out when one ray is rotated about the vertex to coincide with the other (see “Measuring angles”, below). Where there is no possibility of confusion, the term “angle” is used interchangeably for both the geometric configuration itself and for its angular magnitude (which is simply a numerical quantity).
And another definition says:
A shape formed by two rays sharing a common endpoint or two lines that intersect. An angle has one vertex and two sides.
So before we are done with all this our ontology will have to include fundamental geometry, including rays, endpoints, vertices, length (which we’ve previously covered), lines, and intersection. Here we are going to deal with nothing more than how angles are measured and pi.
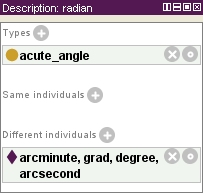
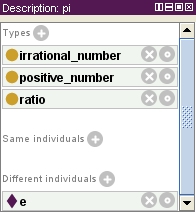
Angles are measured in degrees or radians. Radians may seem strange at first but they are harmless. The ratio of a circle’s circumference to its diameter is the same, regardless of its radius (which is half its diameter, of course). This is really no big surprise, since the ratio of a square’s circumference to the length of its sides is constant, too. Unlike a square, where the ratio is the number of sides (i.e., 4), the ratio of the circumference of a circle to its diameter is an irrational number, called pi.
Is pi a fraction?
Most of us know that pi is approximately 3.1415. It is also true that the digits after the decimal point continue forever without a repeating pattern. Numbers that cannot be expressed with a mantissa that is either finite or repeating are called irrational numbers. If a real number is not irrational then it is rational. There are also complex numbers that mix real and imaginary numbers (involving the square root of negative one), but we’ll skip those for now, OK?
Rational numbers are not irrational
Rational numbers are normal fractions, one integer over another. Any rational number that is not equal to an integer has either a limited mantissa or a repeating pattern. For example, the mantissa of ½ is a single digit, as in 0.5. The mantissa of ¼ is two digits, as in 0.25. The mantissa of 1/3 is an infinite number of digits, all of which are 3, as in 0.33333…. The mantissa of 1/7 is a little more interesting. It is a repeating pattern of 6 digits, as in 0. 142857142857142857142857142857142857…
So our ontology of numbers includes both rational numbers (i.e., fractions) and irrational numbers and pi is an irrational number. But recall that rational numbers and irrational numbers are disjoint. That is, a fraction cannot be an irrational number. So pi cannot be a fraction!
Ratios are not fractions
Fractions are the ratio of one integer to another. Not all ratios are between integers, however. In fact, some ratios are between amounts, such as an amount of distance per an amount of time (e.g., miles or kilometers per hour).
Pi is not a fraction because the circumference of a circle is not an integer. But more generally, a fraction is a ratio but not all ratios are fractions.
Angular units
An angle of one radian covers an arc of circle that is equal to the circle’s radius in length. Since the diameter is twice the radius in length and the circumference of a circle is pi times its diameter, there are 2 times pi radians in a circle.
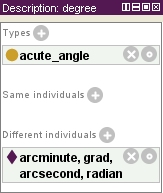
A degree is also an angle. More precisely, there are 360 degrees in a circle. And each degree equals 60 seconds of an arc. And each second of arc has 60 minutes. Thus, a second of arc is 1/3600th of a circle.
Acute and other angles
So, a radian is a little more than 57° and both a radian a degree are acute angles. All of these units of angle are therefore acute, which means that they are less than a right angle (which is 90°). An angle of 180° is called a straight angle and an angle between a right angle and a straight angle is called an obtuse angle. And an angle that is more than a straight angle is called a reflex angle (they are commonly used to express a heading or bearing).
Pi at last
So, pi is a positive, irrational number and the ratio of any circle’s circumference to its diameter, as shown below.
Note that e is Napier’s constant – the base of the natural logarithm (i.e., ln(x) = loge(x)). It is another positive, irrational number that is distinct from pi. These are, practically speaking, the only two irrational numbers most people will ever come across in math or physics. In fact, most people know pi but never use it. Relatively few know or use e, but you need to know the natural logarithm in mathematics class or if you hope to get college credit for physics with high marks on the AP test.
[1] As noted previously, I’m also suspect on “their” choices concerning electricity and chemistry.
[2]If a topic evokes discussions like this one, it’s out! (As is anything that includes the word “corpuscular”, OK?) The total size of this thing cannot be thousands of concepts. As many relations (which includes properties, predicates, etc.) as it takes, but hopefully closer to the order of a hundred concepts – maybe less. Yes, Viriginia, that means chartreuse is out!


A few errors and quibbles, plus one fundamental disagreement:
1.) One second of arc is 1/(360*60*60)th = 1/1,296,000 of a circle, not 1/3,600.
2.) Ratio vs fraction – you assume fractions allow only integers for numerators or denominators but this is true only in the simplest maths and not at all in physics or chemistry. The point of SI (or other unit systems) is that everything has an explicit unit or an explicit lack of a unit, so almost no calculations are done against bare numbers. Your distinction between fractions and ratios here does not seem to serve your argument. However, I certainly agree that a ratio can be between any two related quantities, whether the result has an explicit or implicit unit or not.
Finally,
3.) I have a basic disagreement with your statement: “… the physicists and chemists who defined the the International System of Units overlooked [angles].” SI was intended to define units and relationships unambiguously to replace the hodge-podge of units and measurements that existed in different locations prior to the French Revolution. The radian was an SI supplemental dimensionless unit until 1995, after which it was relegated to a derived unit. Same goes for the steridian.