Understanding events and processes takes time

We have been teaching a computer to answer questions like, “How much did IBM’s earnings change last quarter?”  It takes a fair bit of knowledge, including how to understand English, to answer this question.  But teaching it what a “quarter” is brought back memories of debates with some former CMU colleagues about what units are and how to model time.  Since quite a few people ask me for help with knowledge engineering and ontological matters, I thought some might be interested in parts of those debates.As you will see, a strong upper ontology of common knowledge is required to understand common business knowledge.  Leveraging such an ontology is the only way to deliver business rules for under $50.

Sentences like “do something if more than a number of possibly related things have happened within a timeframe of something else happening” or “do something if nothing happens within a timeframe following something happening” are extremely common in business process management (BPM), complex event processing (CEP), and workflow.  With a sense of time, a business rules management system (BRMS) can support BPM, CEP, and workflow applications almost trivially.  Without a sense of time, most BRMS force users to perform computations.

For example, without a sense of time and an infrastructure that supports it, the sentence “call a customer if no response is received within 30 days of notifying the customer of a delinquency” has to be transformed into something like “if a notice is mailed on a date and the notice is a delinquency and the date of notification has a day number then compute the date for checking by adding 30 to the day number and check for a response to the delinquency notice on the date for checking”.  The checking on a date for a response to a notice must also be implemented as a database (or persistent queue) of events to be polled or triggered by application code.  Then a second rule is required to implement the check, as in “if checking whether a response has been received to a notice and the notice was given on a date of notice and the notice was given to a customer and there exists no record of communication with the customer since the date of notice then call the customer”.  (Note that this is actually how most BRMS products would implement this.  The natural language approach I prefer handles the original sentence.)

The discussion here reflects the general structure and content that a usable ontology for business process management requires.  Most users of business rules management tools will find the need to understand and engineer this discussion in their tool of choice.  As my Haley Systems customers know, much of this is reflected in Authority’s built-in ontology and English vocabulary, but quite a few of the points discussed here reflect improvements, especially concerning the confusion between units and amounts.

As you will see the discussion takes careful thinking.  Some readers may find it onerous.  If at any time you have had enough (or if you simply cannot take anymore!), please skip to the end and decide whether to fill in the conclusions by revisiting the body.

As an introduction, consider whether:

• A unit is an effectively constant amount suitable as a reference for measurement.
• A month is a unit.

Months and years

It seems obvious enough that a quarter is one fourth.  That is, a quarter is one fourth of a year, or three months.  But how long is a month?

Typically, when we say a month, we are thinking about a month on the calendar, not a lunar month.  The number of seconds in a lunar month is almost constant over centuries.  For calendar months, the number of days varies between 28 and 31 and the number of seconds follows.

Note that a month on the calendar may not correspond to a month of the year, each of which has a proper name from January to December.  A month from April 15^th, for example, would be May 15^th.

So at this point there are three different kinds of months that we can model:

1. lunar months
2. calendar months
3. months of the year

We can also model twelve instances of months of the year.

When we say, “a month from now”, we can mean thirty or so days from now or the day within the next calendar month that is closest in number to today.  That is, a month from January 31^st is either early in March or the last day in February.  A reference to a month from March 31^st might mean May 1^st, but more typically it would mean the last day of April, the 30^th.

Calendar months are aligned within calendar quarters which are aligned within calendar years.  A year can begin on any day, such as a birthday or other anniversary.  A year on the Gregorian calendar, on the other hand, always begins on the first day of January.

Just modeling days, months, and years, including the months of the year but skipping lunar months, is a good start.  But don’t forget quarters and whether years or months are aligned with the calendar.

Time intervals

The machine should also understand that a period of time begins at a point in time and ends at another point in time that does not occur before the beginning point in time.  It should also understand that the duration of period of time is a length equal to the difference between its endpoints.

Interestingly, the beginning and ending times of a period have a position along a timeline but they do not have units.  The difference between the beginning and end of a period does have a unit, however.  The unit measures an amount of time.  For example, a month is a period of time.  The difference between the beginning and end of any month is an amount of time that can be measured in seconds or days.

Points in time

Some would suggest that points in time can be viewed as intervals of time of zero length.  Although this may be mathematically fine, it is not appropriate semantically.  Few would argue that a point has a beginning or end.

Points in time occur before or after other points in time, including the beginning and ends of time intervals.  A point in time occurs before a time interval if it occurs before its beginning.  A point in time occurs after a time interval if it occurs after its ending.  If a point in time is neither before nor after a time interval then the point occurs within the interval.

Incredibly, most rules engines do not understand that the difference between two times is an amount of time.  They cannot deal with trivial statements such as “if it has been more than a week since something happened” unless somebody programs them with special predicates.  It is much better to understand more generally that adding an amount of time to a time produces a time that cannot be earlier.

If you are following along and trying to build your own ontology of time, make sure you define a general concept of time above periods of time (aka time intervals) and points in time (aka instants).  Add the beginning and end of time intervals.  Also, model amounts of time (i.e., durations), which do not begin or end.  Then model the functional relation between a time interval’s beginning, end and duration (i.e., given any two the third is determined).  Then add the basic ordering relations of time.  That is, model points or intervals that occur before or after each other.  Then model points or intervals occurring during a period of time.  You might also want to add a few more relations about overlapping or adjacent time intervals.

After you are done, try to model the concepts from the previous section.  You may experience some difficulty with the notion of a month beginning at a point in time.  That is, every January does not begin at the same point in time.

Which January?

When we say, “It’s usually cold in January”, we are referring to a month of the year, but without regard to any specific year.  If we say, “It was unusually cold in January, 2008”, we are referring to a month of a specific year.  The former refers to a month that occurs every year.  One could argue that that a month of the year is not a month at all since there are many such months, not just one (i.e., there have been many Augusts).  January, 2008, on the other hand, was definitely a specific month.

As you will see, understanding this is critical to answer the original question, “How much did IBM’s earnings change last quarter?”.

Periodic time

The months of the year are periodic months.  They occur repeatedly or, in other words, they recur.  In general, months are periodic, whether or not they are lunar months, calendar months, or months that do not begin on the first of a month of the year.

Days, like months, are periodic.  A date on the other hand refers to a day of a month of the year.  If a date also includes a year, then the date refers to a specific day.  Without a year, a date refers to a day of the year.  A day of the year occurs in a month of the year.  Days of the year, like months of the year, are periodic.  That is, a day of the year occurs every year (ignoring February 29^th for simplicity for now).

By distinguishing specific from recurrent periods of time, the latter having duration but only the former having a beginning or end, the days, months, and years we originally modeled can be organized as recurrent periods of time.  Dates can be modeled as specific periods of time (pending a discussion of time zones, below).

Note that periodic intervals of time need not be contiguous.  Months of January are periodic but there are gaps in time between them.  Months on the other hand form a segmentation of adjacent and abutting time intervals that are aligned with and partition yearly intervals of time, which is discussed further below.

Although important, the notions of points or intervals or lines are not understood by existing business rules management systems (BRMS) or BPM / CEP tools  Without such notions, the tools cannot understand sentences or solve problems that involve reasoning over time.  This makes them harder to use or ineffective for common problems.  For these reasons, an ontology that covers time is important.

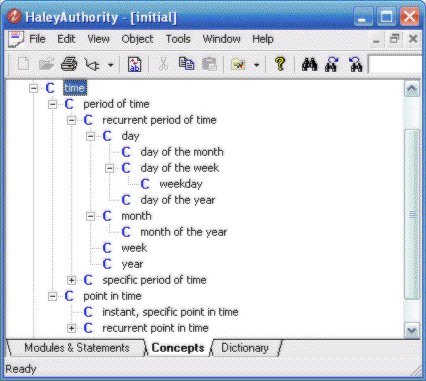
Here’s a peak at how it was done in Authority:

The labels here are singular common count noun phrases omitting their determiner (i.e., “a” or “an”).  Note that Authority does not model lunar months so it omits the adjective “calendar” from in front of “month”.  It should have a concept for a calendar year, however.

An ontology includes relations in addition to concepts.  In Authority, such relations are labeled by phrasings to support natural language processing, as shown here:

Authority seems to be missing that an instant may occur during a specific period of time.  Also, personally, I would prefer that these phrasings were more precise semantically, which would also make them less ambiguous, as in:

• a period of time may occur during another period of time
• each period of time must begin at an instant

It would also be nice if mutual exclusivity was understood or expressed, as in:

• an instant during a period of time cannot be before or after the period of time
• a period of time must end after it begins

The following shows how a specific period of time is defined in Authority’s ontology.

Ideally, the ontology should have a more abstract notion of lines and intervals (i.e., line segments) from which periods would inherit.  In that case, it would be understood that one line segment could occur within a second and the phrasing above would be more generally understood.  It would also be better to know that a period’s duration is the length of its time interval and that the length of an interval or line segment is the difference between its beginning and end.

Days of the week

We touched on periodic time above when discussing the difference between January, in general, and January in a specific year, such as 2008.  As with months, the days within each week are also named, as in Monday through Friday, Saturday, and Sunday.

• a week is seven days long

When we talk about this Friday, we are referring to a day that has a date.  That is, we are referring to an instance of a day.  That is, we are referring to a particular or specific day.

Thus, the ontology should include the days of the week.  This was modeled as shown below in Authority:

The redundancies of the first and last pair of sentences reflect Authority’s lack of understanding of that “of” can be used for “within”, which is reduced to “in” above.

The redundancy in the middle pair indicates deeper limitations of Authority.  The middle pair should not be required given the first and last phrasings, for example.  The redundant use of “day of the week” is certainly awkward.

How would you model a weekend versus weekends?  Analysts commonly consider how many days off occur in a month when considering retail sales or travel figures, for example.  When is a weekend a three day weekend?  Do weekends begin on Friday?  When does the weekend begin during the week of Thanksgiving?  Do weekends ever begin or end on different days in different countries?

There are always two days

Practically speaking, years generally refer to specific years, but months and days are quite ambiguous.  A day that falls in a month, for example, may refer to a specific day or a day of the year, as in March 15th with or without a year.  Even specific days, and therefore months and years are ambiguous, however!

January 1^st begins earlier in Hong Kong than it does in New York.  The same is true of January, February and March.  The same was true for 2008.

Any specific time, whether it is an instance or an interval, may be local or universal.  It is important to understand and respect the difference.  Noon in Universal or Greenwich Mean Time (GMT) occurs only once each day.  Midnight occurs 24 times each day, ignoring any peculiar time zones.  That means a date, which almost never includes a time zone, could refer to any of 24 intervals of Universal Time.  Rather than analyze local versus universal time here, we ask the interested reader to ponder whether a time of day in any specific time zone occurs on two different dates and:

• each local day begins at midnight
• noon occurs each day at 12:00:00pm local time

Note that the preposition “at” is used to refer to an instant as a position, which is consistent with the view of time as space discussed previously.

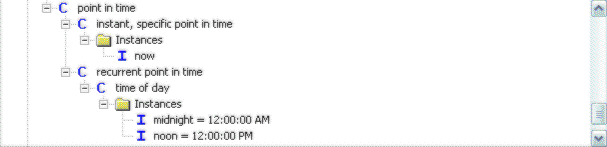
Times of the day occur each day, so they are recurrent.  And “now” refers to a specific point in time that moves through time.  Now is a tricky case that could be modeled differently, but this is how we did it in Authority:

Note that midnight and noon do not specify a time zone.  Time of day should have local and universal specializations.  A universal time of day would require a time zone.  In this way, 5pm EST or midnight GMT, which are each certainly times of day, could be specified even though they occur at different local times of day in different time zones.

The ontology should also include time zones, of course.  Then it could represent the following:

• every local time of day within any time zone occurs at one universal time of day
• every universal time of day occurs at one local time of day in each time zone
• every instant occurs at one local time of day within each time zone

Also note that dates can be specified with a time zone.   Thus, even periods of time can be local or universal.

• every instant occurs on one date within each time zone

Do quarters vary by time zone?  Is it relevant to “How much did IBM’s earnings change last quarter?”?

Spatial time

Parenthetically, we referred to the duration of a time interval as a length above.  That is, when we talk about a length of time we are viewing time as a line from one point in time to another point in time.  Note the interesting use of the preposition “in” rather than “on”.

A proper understanding of time requires an understanding that it is a linear dimension that has segmentations which have further segmentations.  Time is segmented into calendar years each of which is segmented into calendar months, each of which is segmented into days which are further segmented into hours, minutes, and seconds.  A deeper understanding of position and the transitive nature of containment of instants within dates within specific months within specific years, can eliminate many of the redundancies and complexities of the relations and phrasings shown above

Ordinal time

A proper understanding of time also leverages our knowledge of ordinal positions within a sequence, which in turn relies on our knowledge of integers and their order.  January is the first month of the year and December is the twelfth.  December is also the last month within a calendar year.

Understanding ordinals is also important in understanding days of the month.  For example, I am not aware of any tool that understands whether something occurs before or after a day of the month, as in “a date after the 15^th“.  This results in a burden on users to remove ordinals by awkward translation, as in “a date for which the day of the month is greater than 15”.  Needless to say, this limits such tools to technical users in many cases.

Note that there is a deep relationship between our notion of order and the passing of time.  For example, we tend to count things from left to right.  When we refer to the first, we are usually referring to the leftmost while the rightmost is typically called the last (unless the last is closest, in which case it may be called the first).

Parts as units

Practically speaking, months always begin at the beginning of their first day and end when their last day ends.  They do not start or end in the middle of days.  Similarly, quarters begin at the beginning of their first month and end when their last month ends.  There are first, second and third months within each quarter and each year has a first, second, third and fourth quarter.

• a quarter is three months long
• a year is twelve months long
• a year is four quarters long

Note that we have measured a year in terms of months or quarters, even though months and quarters are not all of the same length (i.e., duration).  This begs the question, “what is a unit?”, and whether a unit should be a constant, reference amount.

Units as constants

Somewhere along the way a quarter of a lunar month became a week and quarters of the solar year became the seasons, aligned on the solstices.  We observed that lunar months did not exactly correspond to 28 days and there are more than 365 days in a solar year.  As astronomy advanced, we realized that the period of earth’s rotation was a day, that the period of the moon’s revolution around the earth was a lunar month, and that the period of the earth’s revolution about the sun was a year.  Along the way we fit an even number of calendar months into calendar years, which the Gregorian calendar aligns with solar years using leap days.

Since the length of days, lunar months and solar years are constant within the perception of a human lifetime; they are effectively units of time.  Even a calendar year, like a calendar month, is not a constant amount of time, however.  Nonetheless, it is more practical to consider a calendar year a unit of time since its variability is less than one thousandth.

Months, on the other hand, vary by over ten percent, such as between January and most months of February.  Such variability hardly seems consistent with our notion of units as effectively constant amounts for reference in measurements.

Much versus many

We use “how much” with mass nouns and “how many” with count nouns.  Units measure how much stuff is on hand.  Numbers without units count how many things are on hand.

We use units to convert from how much stuff to how many units of stuff.  In effect, units divide a quantity of stuff into countable parts.  Units, like other nouns that divide things into parts are called partitives.  For example, in “three buckets of water”, a bucket is used as a partitive.

Partitives are usually count nouns (i.e., they have singulars and plurals) since the result of partitioning is a something countable.  In English, they occur commonly before the preposition “of” followed by a mass noun; as in, “a yard of rope”, “a gallon of milk”, or “a ton of steel”.  There are other interesting cases, too, such as “a pound of nails” and:

• a month of the year
• a day of the week
• an hour of the day

Clearly, units are partitives.  But not all partitives are units.  Consider the partitive in “a member of the community”.  Other partitives may seem more like units because measurement is ambiguous with regard to precision.  For example, we can conceive of an amount of bread in terms of pieces or loaves, but we cannot determine how much bread a number of pieces or loaves of bread refers to without measuring weight or volume more precisely.

Understanding the spatial and ordinal aspects of time is relevant to understanding “last” in “How much did IBM’s earnings change last quarter?”, although we will not pursue that in detail here at this time.

Monthly partitions

If a whole is divided into parts it has been partitioned, even if the parts are not of precisely the same size.  Set theoretically, a partition of a set is a union of disjoint subsets that cover the set.  Semantically, a partitive breaks a mass into individual parts each of which hold some of the mass but without any of the mass being in more than one part and the sum of the parts equally the original mass.

If a line is partitioned, the resulting parts are line segments that cover the line without gaps or overlaps.  Each segment begins either where the line begins or where another segment of the line ends.  Each segment ends where the line ends or where another segment of the line ends.  The segments cover the line.  But the segments may not be of equal length.

Understanding partitions is very important for reasoning about time and space.  For example, a date falls in only one calendar month or year.  We partition time into years, each of which is effectively the same length.  We partition years into months which are not of the same length.  The same is true of quarters.  Quarters partition years but have slightly varying numbers of days.  This supports the argument that months and quarters may be partitives but they are not units.

Units are amounts

Unfortunately, as shown below, Authority models a month as a unit.

This is unfortunate not just because a month includes a variable amount of time, but because Authority is confused about the difference between amounts and units.  The arguments first mentioned above about months were nothing compared to arguments about the difference between units and amounts – or lack thereof!

According to the American Heritage Dictionary, a quantity is an amount or number or refers to some measurable, countable, or comparable aspect of something.  This is reflected in Authority as:

Note that Authority does not understand that a day as an amount of time!

Is there a difference between an amount and a unit?  How would you model them?

Perhaps a day should also be understood as an instance of an amount of time?  If so, the same instance should be knowable as 24 hours, where an hour is another amount of time that is also knowable as 60 minutes.  The instance of an amount of mass (on Earth) of 1 ounce should be knowable as 28.349 grams, where a gram would also be an amount of mass, of course.  This would be particularly helpful for more complex units, such as temperature.  The boiling and freezing points of water expressed in Celsius and Fahrenheit and knowledge that that each is a linear measure is all that is needed to understand how to convert between them.

The concept of a unit is not unreasonable.  For example, Decibels and the Richter Scale are logarithmic scales used to measure relative amounts using an exponent and a reference point.  Power is typically measured using such scales, but it can be any kind of amount (in both the numerator and the denominator).  In computing the ratio the units cancel.  Such a ratio could be modeled simply as a number rather than as a unit, however.  In any case, units that are not unit-less are amounts.

Unit agreement

Amounts are measurable rather than countable quantities.  If you divide an amount of time by an amount of time you get nothing more than an integer or real number.  This is true not just for time, but for any measured “stuff”.  For example, speed is distance over time.  If you divide one speed by another you get a number that does not involve time or distance.  If we divide by one mile per hour, we can express one speed as a number of miles per hour.

Months are for counting, not measuring

Perhaps the acid test for a unit is whether it can be used as a dividend to produce a number.  I think months fail this test, too.

How many months are there in 100 days?  If you divide one month by another month do you always get one?

The bottom line is that months are recurrent periods of time but they are not specific amounts or units of time.

Quarters, finally!

So if months are recurrent periods more than amounts of time, then quarters, which consist of three months, but whose duration vary by more than one percent (1%) should be nothing more than recurrent periods that are partitioned by months and which partition years.   Unlike months, however, it is important to distinguish between quarters that are aligned with calendar years.  That is, a calendar quarter should be modeled as a specialization of a quarter since not all quarters are aligned with the calendar year.

In order to properly answer questions such as, “How much did IBM’s earnings change last quarter?”, it is necessary to understand that a corporation’s fiscal year is not necessarily aligned with the calendar year.  Therefore, we should model that a calendar year is a specialization of a year and that a calendar year is partitioned by calendar quarters which are partitioned by calendar months.

Note that a fiscal quarter may specify a day of the year (i.e., a recurrent date, that is, a date without a year) on which the quarter ends.  Depending on your purposes, it may be safe to model a fiscal year as ending on the last day of a month, in which case only the month of the year, not a specific year or day of the month could be modeled.   If not, fiscal months will not be calendar months, of course..

Finally, even time zone considerations may be required.  A corporation that operates in multiple time zones may accrue revenue or expenses when the occur in headquarters time zone.  If so, its fiscal quarters end at different local times in different time zones.  If the corporation is a global corporation, one of its time zones will have a different date.  In this case, the end of a fiscal quarter could be specified as a universal date (i.e., a date with a time zone) or, less ambiguously, a universal time (i.e., with a time zone).

As you can see, it takes a lot of ontology to understand common concepts.  But once you build a strong upper ontology, you will find great flexibility in the resulting power of reasoning and problem solving.  You will also find that it takes less effort to accomplish more as your ontology includes time, money, process, and some of your more domain-specific knowledge.  This is the basis of the $50 business rule.

[ratings]