Deep learning can produce some impressive chatbots, but they are hardly intelligent. In fact, they are precisely ignorant in that they do not think or know anything.
More intelligent dialog with an artificially intelligent agent involves both knowledge and thinking. In this article, we educate an intelligent agent that reasons to answer questions.
The agent’s knowledge is expressed in simple, English sentences. The agent reasons using informal logic from those sentences and pragmatic knowledge about how to interpret and answer questions.
- The domain for this intelligent agent is decision support for compliance with sales tax laws and regulations.
- A pragmatic framework demonstrates simple reasoning beyond chatbots using an open-source reasoning system.
In combination, we demonstrate how the following types of reasoning can be easily incorporated into intelligent agents:
Other posts and pages address these topics and the use of natural language knowledge acquisition, representation, and reasoning more formally. This is a casual, introductory post aimed at making the lower end of the intelligent agent spectrum (i.e., chatbots) smarter.
- if you are more interested in policy automation, decision management, or compliance, you might be more comfortable starting with this introduction to logical English or the 2-part confessions of a production rule vendor.
Simple Knowledge Acquisition
For simple sentences, natural language processing (NLP) systems can frequently produce knowledge representation that is sufficient for effective question answering beyond chatbots. For example, the following results immediately from parsing a simple sentence.
This knowledge representation is much simpler but not much less practical than fully-specified predicate calculus. The important thing is that it gives us a structure representation that we can work with using the machinery of logic programming and notions such as textual entailment. If you’re interested in the details and how to go further towards “axiomatic knowledge”, please see the notes. [1][2][3] The Linguist can make many reliable deductions not shown above, but let’s stick with this most simple use case for purposes of this post.[4]
The most basic question is what the sentence means. Then we can consider how its meaning is to be used in reasoning (e.g., to answer a question, support a decision, etc.).
Our common sense tells us that the intended meaning here is that food products and medicines do not intersect (i.e., they are disjoint; having no common members).
- So how would we want to reason with this understanding?
We could ask abstract questions about food products or medicines as types of things. Or, we could ask questions about a specific food product or medicine.
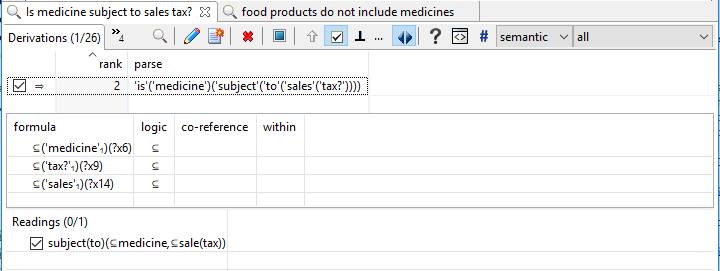
For example, we could ask “Is medicine subject to sales tax?” where we know that food products are not subject to sales tax.[5]
Note that the system understands that the above is an interrogative sentence (i.e., a question).
The following, on the other hand, is a declarative sentence:
But, of course, the answer to the question would be “I know nothing that is subject to sales tax.” At least until we say something like:
Intelligent Agents’ Inference Engine
In order for the logic of the interrogative and declarative sentences above to be used by an intelligent agent, its representation must be made available to some type of inference engine.
Assuming we have loaded results from the Linguist into Flora-2, the following query:
- flora2 ?-reading(of(sentence))(?reading,?_)@parse.
Has the following answers (the question is underlined):
- ?reading = subject(to)(‘⊆'(medicine),’⊆'(sale(tax)))
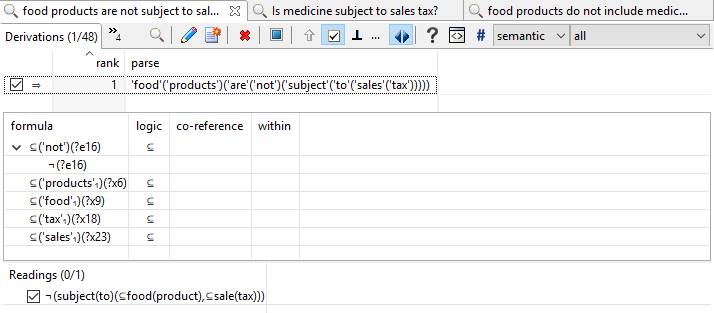
- ?reading = ‘¬'(include(‘⊆'(food(product)),’⊆'(medicine)))
- ?reading = ‘¬'(subject(to)(‘⊆'(food(product)),’⊆'(sale(tax))))
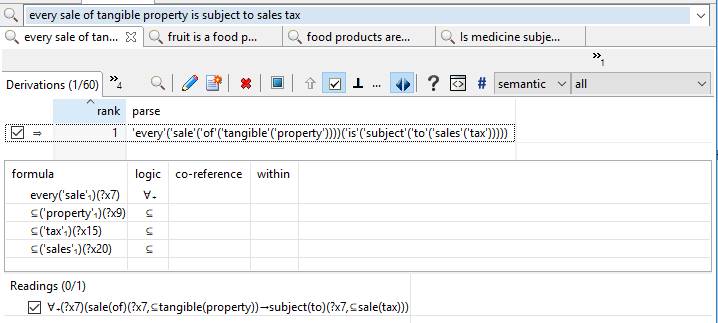
- ?reading = ‘∀₊'(\##7)(‘→'(sale(of)(\##7,’⊆'(tangible(property))),subject(to)(\##7,’⊆'(sale(tax)))))[6]
Here, \## introduces what Flora calls a skolem constant. For our purposes here, you can think of these as variables. The fact that they are constants in Flora merely prevents their undergoing unification.[7]
Identifying Pertinent Knowledge
Now we can look at the atomic formulas[8] of these readings using the following query:
- ?- reading(of(sentence))(?_reading),atom(of(reading))(?atom,?_reading).
To which the following answers are received:
- ?atom = include(‘⊆'(food(product)),’⊆'(medicine))
- ?atom = sale(of)(\##7,’⊆'(tangible(property)))
- ?atom = subject(to)(\##7,’⊆'(sale(tax)))
- ?atom = subject(to)(‘⊆'(medicine),’⊆'(sale(tax)))
- ?atom = subject(to)(‘⊆'(food(product)),’⊆'(sale(tax)))
These suggest that the readings that contain atoms about \##7 or ‘⊆'(food(product)) being subject to sales tax may be pertinent.
Matching atoms from the question with atoms from the readings suggests 2 further deliberations:
- Could ‘⊆'(food(product)) include ‘⊆'(medicine)?
- Could ‘⊆'(medicine) and \##7 intersect?
The answer to the first is given by the reading that negates the pertinent atom (i.e., food products do not include medicines).
- The answer to the second deliberation involves metonymy.
Note that the sentence about sales of tangible property is about the sale rather than the property but the question seems to be about medicine as the property involved in a sale. This is an example of metonymy. The question is not whether some medicine in a bathroom cabinet is subject to tax but whether a sale of medicine is subject to tax.
Metonymy
Answering questions requires handling metonymy. It’s practically impossible for human beings to avoid using metonymy. It is pervasive.
- All we know about sales tax from the above sentences is that sales may be subject to it.
- Presumably, we would not say that something that is not a sale is subject to (or not) sales tax.
This suggests that we abductively infer that the question is about a sale of medicine and that the statement excluding food products from sales tax is about sales of food products. Alternatively, if we do not assume (as in abduction), we can ask.
One again, we have narrowed the question answering process to the following point:
- subject(to)(\##7,’⊆'(sale(tax)))
- →'(sale(of)(\##7,’⊆'(tangible(property))),subject(to)(\##7,’⊆'(sale(tax)))) where
- \##7 matches ‘⊆'(medicine) from our question
The implication would hold if \##7 was a sale of medicine.
- To resolve the metonymy, we take one step away from medicine.
- In this case, we move to something about medicine.
Let’s make this a little easier… the following answers result from simplifying the prior answers:
- ?simplify = sale(of(‘⊆'(tangible(property))))(?X7)
- ?simplify = subject(to(‘⊆'(sale(tax))))(?X7)
- ?simplify = subject(to(‘⊆'(sale(tax))))(‘⊆'(medicine))
- ?simplify = subject(to(‘⊆'(sale(tax))))(‘⊆'(food(product)))
Note that the antecedent of the implication is italicized above (the question remains underlined).
Abductive Inference
When we consider metonymy, we simply allow for some function of the phrase used, as in:
- subject(to(‘⊆'(sale(tax))))(?F(‘⊆'(medicine)))
Unifying this with the 2nd answer above yields:
- ?X7=?F(‘⊆'(medicine)))
Given the implication above, the answer would be yes if ?F resolves the metonymy, as in:
- holds(sale(of(‘⊆'(tangible(property))))(?F(‘⊆'(medicine)))))
In general, a predicate that holds for something general holds for something more specific, as in:
- holds(?predicate(?p(?X))(?predicate(?p(?Y))) :- preposition(?p), subsumes(?x,?Y).
Ontology and Common Sense
Our objective in this article is to simply convey how a little knowledge representation and inference is the difference between a chatbot and an intelligent agent. There is more to cover about how an intelligent agent gets domain knowledge, such an understanding of products and services offered by an enterprise. That commonly involves reading pertinent documentation to extract and align domain-specific vocabulary and ontology. Here, we admit, that we gloss over all that. In a future post we will show how we do that, such as we have done for cooking.
If we have loaded an ontology or written a sentence to the effect that tangible property includes medicine, we will deduce the prior statement.
- We can deduce that medicine is tangible by reading using common sense, such as:
- This leads us to a better ontology where we educate the machine about transfers of ownership of property (i.e., sales).
Obviously, there is much to go into here about the agent’s knowledge, inference capabilities, and reasoning heuristics. We will make the simple claim that a small body of general pragmatics combined with sufficiently precise knowledge from domain documentation can produce a smarter agent than deep learning can obtain with Big Data. The differences are:
- A chatbot may respond as if it understands but cannot answer questions if any reasoning is required.
- The chatbot has no explicit, reliable knowledge and does not reason.
- [Yann] LeCun, head of AI at Facebook: “what’s still missing is reasoning”
- An intelligent agent has some knowledge with which it does reason.
Learning or Clarifying by Asking
Unlike a chatbot, an intelligent agent engaged in dialogue may wish to clarify the intent of a question or even ask for help in figuring out the answer to a question.
If we have neither loaded an ontology nor read enough to deduce that medicine is tangible, the agent could ask… depending on the user, their goal, and the context of the interaction.
In XSB and Flora, we have the well-founded semantics[14], which allows us to express the following:
- subsumes(?x,?y) :- \neg subsumes(?x,?y), ask(subsumes(?x,?y)).
Which invokes the action to ask only if it is not already known or provable (positively or negatively) that one subsumes the other. (This is different from Prolog’s strictly procedural behavior).
Putting It Together
In either case, once we have that the metonymy around medicine can be resolved by:
- ?F=sale(of(?_))
We answer the question by deducing the following:
- subject(to(‘⊆'(sale(tax))))(sale(of(‘⊆'(medicine))))
Typically, we resort to metonymy when no answer is found without it. So we ask the question without metonymy and, if no answers are obtained, we pursue the question again, this time allowing metonymy.
Of course, in an actual dialog, we might ask for confirmation of the metonymy and, in either case, render the confirmations and answers above as English sentences.
For example, the agent might say any of the following:
- Yes.
- Yes, a sale of medicine is subject to sales tax.
- Yes, if you were asking about sales of medicine.
As simple as this example may be, it demonstrates general techniques, just a few of which allow an agent to be more intelligent than a chatbot. All it takes is a little thinking (i.e., knowledge and reasoning).
[1] Bunt, Harry. “Semantic under-specification: Which technique for what purpose?.” Computing meaning. Springer, Dordrecht, 2008. 55-85.
[2] We ignore the quantifier for “food” here but could establish its variable as equal to the variable for products, as is almost universally the case for compound nouns.
[3] We ignore the quantifier for “not” here, which refers to the situation in which the negation holds. In effect, we interpret the negation “universally”.
[4] For example, the Linguist realizes that:
- the focal referent here is the noun phrase headed by “products” (i.e., ?x6)
- e.g., it’s scope is outermost and includes the quantification of ?e16
- e.g., that its quantifier is universal given its referent occurs as plural
- the quantification for a subject of an event typically has wider scope
- i.e., the quantification of ?x6 here has scope over the quantification of ?e16
- that “food products” is a compound noun having a single referent
- e.g., the quantification for ?x9 has the same scope as ?x6
- e.g., the variables ?x9 may co-reference or be unified with ?x9
[5] We can be as precise as necessary here, but for simplicity we will omit the distinction of various taxes and their individuality per jurisdiction.
[6] The Linguist also generates the following Flora axioms for the last reading:
- subject(to)(?x7, ‘⊆'(sale(tax))) :- sale(of)(\##7,’⊆'(tangible(property))).
- \neg sale(of)(\##7,’⊆'(tangible(property))) :- \neg subject(to)(?x7, ‘⊆'(sale(tax))).
The second rule reflects that (by default) something that is not subject to sales tax cannot be a sale of tangible property.
- Most business rule systems would not handle this logic.Flora provides defeasible logic to handle the exceptions.
[7] See this background information or this page at Wikipedia for further information.
[8] definitions for terms of logic can be found here
[10] see this WordNet sense and its definition and hypernyms
[12] see this WordNet sense of sale or this in FrameNet
[14] see this background for more information