Here is a graphic on how various reasoning technologies fit the practical requirements for reasoning discussed below:
This proved surprisingly controversial during correspondence with colleagues from the Vulcan work on SILK and its evolution at http://www.coherentknowledge.com.
The requirements that motivated this were the following:
- First-order expressiveness (i.e., syntax)
- existential and universal quantification
- arbitrarily nested quantifiers and connectives (including implication)
- Support open and closed-world assumptions
- open: explicit deduction/representation of false
- i.e., as in OWL and classical 1st-order logic
- closed: interpretation of “unknown” as false
- i.e., as in business rules systems and SQL applications
- open: explicit deduction/representation of false
- Ensure logical soundness, ideally even with non-monotonicity (i.e., changes)
- Support modality (e.g., “should”/”typically”) and handle inconsistency
- Support 2nd order logic and avoid segregating individuals from types
- Reason within fixed or polynomially bounded time and space
The columns correspond to the following:
- First order logic (FOL) theorem provers
- e.g., Common Logic, OWL-Full, RIF-BLD specification
- Logic programming technologies
- e.g., Prolog
- Description logic
- e.g., W3C OWL-DL
- Business Rules Management Systems (BRMS)
- IBM/Ilog, Fair Isaac/Blaze, Haley/Oracle Policy Automation (OPA)
- Red Hat JBoss Drools, JESS, CLIPS, etc.
- SILK (http://www.semwebcentral.org/) and what Coherent is working on.
A few people got bent out of shape about “logical soundness”. The point here is that most business rules systems and applications disregard logical soundness completely, even though under the hood their algorithms might be capable of supporting logical soundness. For example, ART and Eclipse supported logical soundness for non-monotonic assertions or retractions. So we gave business rules partial credit for logical soundness as well as for non-monotonicity.
There was some controversy about whether Prolog is logically sound. If used correctly, Prolog can be logically sound, albeit not if there is any non-monotonicity. The problem is that Prolog so easily produces unsound results, such as concluding two inconsistent facts, because it has no mechanism for recognizing inconsistency. Furthermore, its implementation of the closed world assumption (negation as failure) combined with Prolog’s procedural behavior in which rule order matters effectively leave the burden of maintaining logical soundness on the application developer rather than an innate characteristic itself. Nonetheless, to appease the Prolog advocates, we gave it partial credit for logical soundness.
A few people got worked up about 1st order syntax versus expressiveness versus semantics. The point of the first line is that you want as expressive a foundation as possible. Ideally, you would also want relational algebra, including the aggregation and sorting operations of SQL, for example, as part of the representational/linguistic formalism supported by your reasoner. But the word expressiveness is hard for some to separate from semantics and semantics is a dangerous word when intellectuals are involved. They have great difficulty with vague use of words that they tend to interpret very precisely. So we changed it to syntax.
- The key point here 1st order semantics, in its most academically formal sense, is impractical. So when we emphasize expressiveness or, more precisely, syntax, we are emphasizing that we want as much as practical of 1st order semantics but that we are willing to compromise on logical completeness in order to remain computational tractable.
There was also some discussion on bounded rationality. Bounded rationality, broadly speaking, is about being able to remain rational within bounded time and space. What it means to be rational is what the theory guys call “the semantics” (the dangerous word mentioned above). They mean what guarantees do you have about what conclusions mean. So bounded rationality refers to having some assurances within bounded time and space. If one cannot deduce that something is true or false within that amount of time or space, the answer will be a third truth value, called “unknown”.
We gave OWL-DL credit for bounded rationality because it is decideable within polynominal time. That’s not a very tight bound, however, so it would be reasonable to give it only partial credit.
There was also some controversy on 2nd order functionality with regard to FOL. Since Common Logic specifies some 2nd order syntax we gave FOL partial credit, even though implementation and use of 2nd order syntax is uncommon with theorem provers (in our collaborators judgement, at least).
Surprisingly, at least to me, was how unfamiliar the theoreticians were with the semantics of business vocabulary and rules specification. SBVR is a strong specification incorporating first order logic with limited modalities that are important in practice. Indeed, looking at the chart, I recall SBVR has provisions for closed world semantics. It’s just not clear enough that SBVR takes an innately open-world perspective. Perhaps someone out there could clarify that?
The team that was involved in the correspondence on this graphic did not include many BRMS folks. The BRMS column reflects that there are different implementation technologies in the market and tries to make a reasonable claim about BRMS in general, although specific BRMS may be green in some cases where there is yellow the same BRMS is likely to be red on another area that is in yellow. Generally, BRMS are strongly biased and most are limited to the closed-world assumption. BRMS typically provide no guarantees of termination (most can easily loop due to their non-logical behavior or forward chain into combinatorial explosions unless crafted to avoid such behavior). Some simpler rule-based systems (especially simple, tabular systems) can provided bounded performance, but they are far too weak expressively and logically to be taken seriously here.
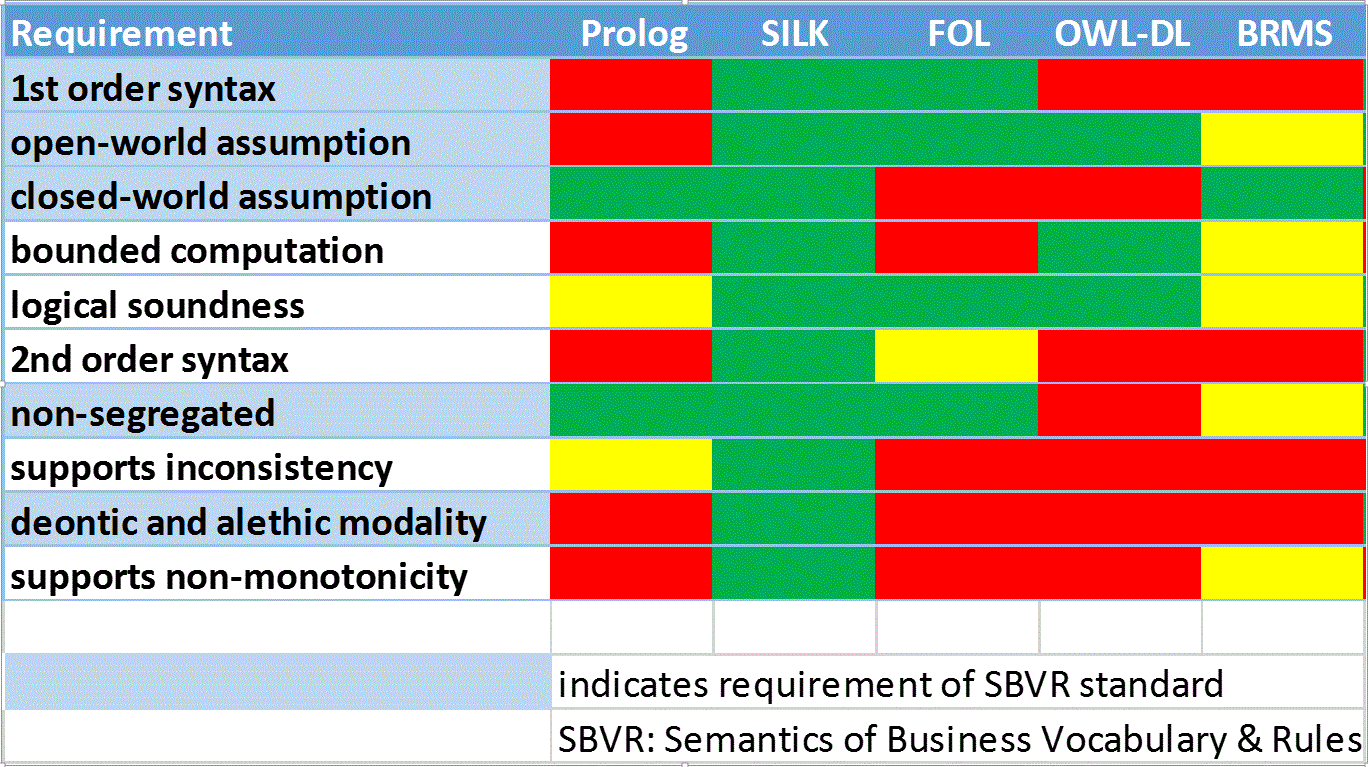
SBVR is based on open world semantics. See clause 10.1.1.1 of the SBVR specification, where it says “The business orientation of SBVR makes it natural to assume open-world semantics by default.” Clause 10.1.1.3 describes and justifies SBVR’s approach to open-world and selectively-closed world semantics in detail.
These clauses claim that SBVR permits selective closure of specific concepts and relationships (“verb concepts” aka “fact types”). Indeed, the first version of SBVR had this capability in clause 8.5 with the verb concepts “fact type is internally closed in conceptual schema” and “concept is closed in conceptual schema”. In recent updates, these verb concepts have been demoted to clause 10.1.2.1, which means they are not actually part of any SBVR vocabulary. I believe this is a mistake because in the real world, some queries do produce concrete answers that can be depended upon. Removing this aspect reduces the expressive power of SBVR.
Thanks, Mark, I forgot about that. This is another area where SBVR is better than many realize. I updated the graphic accordingly.
You may want to take a look at PowerLoom as well (http://www.isi.edu/isd/LOOM/PowerLoom). With the exception of modalities, I think it should cover all of the items in your list. It is a first order logic reasoning system using (mostly) natural deduction. It supports both open and closed world reasoning, bounded computation with some user control, logical soundness, at least some 2nd order syntax (via the “HOLDS” form) and function/predicate quantification, ability to function in the face of inconsistent information, as well a non-monotonicity both by allowing for retraction of information as well as support for defeasible default inferences.
(I was a former PowerLoom developer).