The $50 Business Rule

Work on acquiring knowledge about science has estimated the cost of encoding knowledge in question answering or problem solving systems at $10,000 per page of relevant textbooks. Regrettably, such estimates are also consistent with the commercial experience of many business rules adopters. The cost of capturing and automating hundreds or thousands of business rules is typically several hundred dollars per rule. The labor costs alone for a implementing several hundred rules too often exceed $100,000.

The fact that most rule adopters face costs exceeding $200 per rule is even more discouraging when this cost does not include the cost of eliciting or harvesting functional requirements or policies but is just the cost of translating such content into the more technical expressions understood by business rules management systems (BRMS) or business rule engines (BRE).

I recommend against adopting any business rule approach that cannot limit the cost of automating elicited or harvested content to less than $100 per rule given a few hundred rules. In fact, Automata provides fixed price services consistent with the following graph using an approach similar to the one I developed at Haley Systems.

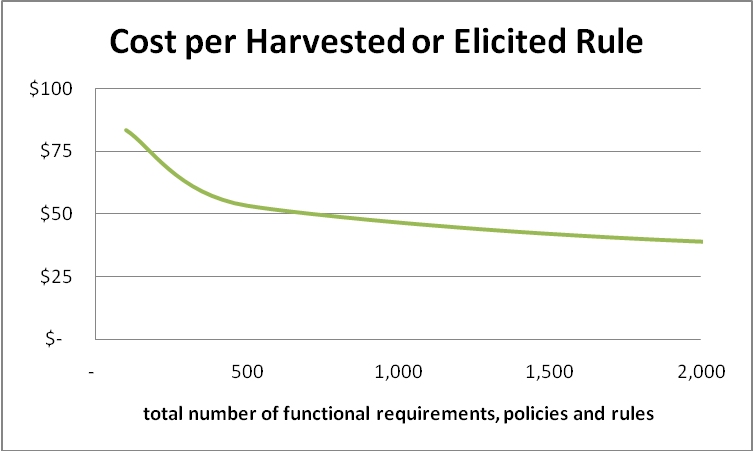
One idea behind using natural language to express formal logic at Haley was not only to deliver agility to business users but to dramatically reduce the cost to implement and maintain business rules during their life cycle. Essentially, the closer we could get the managed form of a business rule to its natural form (i.e., as acquired, articulated or understood by stakeholders and subject matter experts), the lower the cost of reliably implementing and maintaining a functional requirement or policy once it was identified or articulated by regulators or business authorities.The requirement that the managed and automated form of knowledge be close to the natural expressions of stakeholders and subject matter experts required more than just simple natural language, however.

For example, it required understanding and automation of:

• 1. statements without the word “then”, such as “X if Y”
• 2. statements without the word “if”, such as “X [must be true]” or “[it must be the case that] X”
• 3. multiple connectives, such as “X if Y unless Z” and “if A then B otherwise C if D”
• 4. quantifiers such as “only”, “both”, and “multiple” in addition to “each”, “every” and “some”
• 5. aggregates, such as “total” or “average” and ordinal adjectives, like “least”, “oldest”, and “last”

These capabilities do not fit the limitations of

• business rule engines (BRE) or
• logic programming systems or
• the production rule representation (PRR) standard or
• the semantics of business vocabulary and rules (SBVR) standard or
• the rule interchange format (RIF) or
• rule markup language (RuleML) or even
• the general definitions of predicate calculus (e.g., first order logic, FOL) or
• relational algebra (e.g., SQL).

Therefore, we designed a formal representation that extended the predicate calculus with relational algebra. I will write more about such representation in the future. The limitations of database, rule and logic technologies require that the managed content be distinct from the implemented form. As discussed briefly below, this is addressed by generating “extra stuff” that is required to perform the logical or relational functions that may not be supported by any target engine or standard. For now, I would like to focus on the benefits of using natural language to capture, manage and automate business logic.

Applications of business rules start with either:

• documents or an implemented system from which rules are to be harvested or
• stakeholders and subject matter experts from who the necessary business knowledge and functional requirements are to be elicited.

Whichever the case may be, stakeholders and subject matter experts should be involved in potentially iterative reviews of harvested or elicited content, hopefully resulting in confirmation that the captured content appears accurate.

Once the elicited knowledge, requirements, and policies mature to such a point, most business rule technology becomes applicable. That is, the content can be reformulated into the more rigidly structured and less flexible expressive form of if-then rules. Natural uses of words like “total” in phrases like “the total paid within the last 90 days” become complex technical expressions often requiring multiple rules to be written in a manner that will cause them to interact appropriately. Most uses of words like “must” or “unless” have to be eliminated by complex manual reformulation of each confirmed sentence into multiple interrelated rules. And the list goes on.

Suffice it to say that implementing rules in most business rules management systems (BRMS) remains a long row to hoe even after functional requirements and policies have been properly elicited or harvested. Although Authority did better than any other product at minimizing the need for analytic and technical skill in reformulating functional requirements and policies into operational business logic, it did not get to the point that I was satisfied before I took venture capital, after which our focus on my vision of robust automation of increasingly natural language was substantially diminished. I’ll cover some of the needed improvements in subsequent posts.

All is not lost, however! It is fairly straightforward to understand the natural language that Authority understands. For example, Authority’s English syntax roughly corresponds to the following:

• <sentence>
  := “if” <clause> “then” <clause>
  := <clause>
• <clause>
  := <noun-phrase> <verb-phrase>
  := <verb-phrase>
  := <clause> { “if” | “unless” | “only if” | “and” | “or” } <clause>
• <noun-phrase>
  := <determiner> < adjective>* <common-noun>* <count-noun>
  := <noun-phrase> { “who” | “that” } <verb-phrase>
  := <noun-phrase> <function> <noun-phrase>
  := <noun-phrase> <possessive> <noun-phrase>
  := <noun-phrase> { “and” | “or” } <noun-phrase>
  := <noun-phrase> <prepositional-phrase>
  := <number> <unit>?
  := <proper-noun>
  := <time>
• <verb-phrase>
  := <verb> <noun-phrase>? <noun-phrase>?
  := { “is” | “was” } “not”? < adjective>
  := { “is” | “was” | <modal>} “not”? <verb-phrase>
  := <verb-phrase> { “and” | “or” } <verb-phrase>

Note that Authority provides a basic upper ontology, including a taxonomy of concepts and relations between various built-in concepts, including predicates and functions. Authority also provides a built-in vocabulary and phrasings for these concepts, relations, predicates and functions. This lexicon and phraseology is extended as required for any specific application. That is, the <noun>, <verb> and <adjective>-terminals in the above grammar come with a built-in but extensible set of alternatives.

Parsing statements, such as those that can be captured and exported from Authority according to such a grammar is straightforward. Authority itself has roughly the following words for these terminals sketched above:

• <determiner> := “a” | “an” | “any” | “one” | “the” | “some” | “each” | “every” | “no”
• <modal> := “should” | “shall” | “would” | “will” | “could” | “can” | “might” | “may” | “must”
• <adjective> := “total” | “sum” | “other” | “different” | “same” | “last” | “first” | “second” | …
• <function> := “plus” | “minus” | …
• <verb> := <be> | <have> | <do> | <exist> | <multiply> | <divide> | …
• <proper-noun> := January | February | … | Tuesday | Wednesday | …

Authority brings in additional constraints during its natural language processing, such as resolving references when using “the” and determining how prepositional phrases may attach to noun or verb phrases based on the semantics of the underlying ontology. If no semantically plausible interpretation of any syntactically possible parse can be determined, more work is needed before the sentence can be automated. This work might involve rephrasing the sentence, defining vocabulary or phraseology, or improving (e.g., extending) the ontology. If several interpretations of a sentence are plausible, more work is needed to disambiguate the sentence. This typically involves rearranging or adding words to the sentence in order to remove plausible but unintended interpretations. Alternatively, the plausible interpretations can be presented and one can be selected explicitly. In this case, which Authority did not provide, it may even be possible for the system to generate an unambiguous sentence.

Implementing such a parser is a fairly straightforward matter given the underlying information that Authority exports as XML. This export file, which we called KML for “knowledge management language”, includes the text of all the rules, the vocabulary, the phraseology, and the ontology. With this information and a larger, more flexible grammar of English, existing Authority knowledge bases can be re-interpreted into a more robust, engine-independent, underlying logic. Other BRMS, which have much simpler rule languages, require much less sophistication. They are quite easily translated into the same engine-independent logic.

As discussed above, the engine-independent logic needed to support the naturally acquired form of knowledge goes beyond the logic formalisms of rules or SQL or predicate calculus. Whether or not natural language processing is used to produce this formalism, the need for quantification and aggregates as well as exceptions, complex sequential connectives, and action are real but no existing rule or logic system implements all of them. So, it is necessary to translate this more comprehensive and expressive formalism for any target implementation or standard, such as a rule or logic engine.

For example, PRR is limited to forward chaining production rules. It has almost no support for quantification or aggregation while logic programming systems have no support for aggregation or action. Even commercial rule systems are less expressive than SQL aggregation and offer limited quantification and only the simplest form of implication. I’ve addressed some of this in previous posts about requirements and will address it further in the future.

[ratings]