A decade or so ago, we were debating how to educate Paul Allen’s artificial intelligence in a meeting at Vulcan headquarters in Seattle with researchers from IBM, Cycorp, SRI, and other places.
We were talking about how to “engineer knowledge” from textbooks into formal systems like Cyc or Vulcan’s SILK inference engine (which we were developing at the time). Although some progress had been made in prior years, the onus of acquiring knowledge using SRI’s Aura remained too high and the reasoning capabilities that resulted from Aura, which targeted University of Texas’ Knowledge Machine, were too limited to achieve Paul’s objective of a Digital Aristotle. Unfortunately, this failure ultimately led to the end of Project Halo and the beginning of the Aristo project under Oren Etzioni’s leadership at the Allen Institute for Artificial Intelligence.
At that meeting, I brought up the idea of simply translating English into logic, as my former product called “Authorete” did. (We renamed it before Haley Systems was acquired by Oracle, prior to the meeting.)
There were some conflicted parties in the room and a heated debate ensued. I got up to a whiteboard and argued that it was straightforward to extract logic via natural language processing. (I took a few arrows at this point.)
In particular, I wrote down the following sentence and said it was easy to reduce it to axiomatic logic:
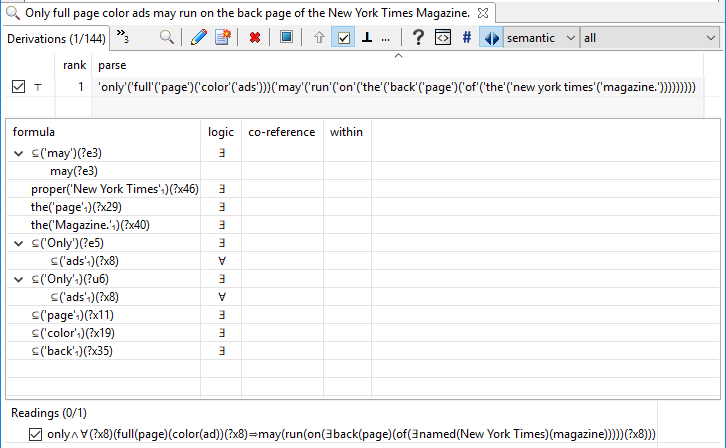
- Only full-page color ads can run on the back cover of the New York Times Magazine.
To fully represent the meaning of this sentence requires an ontology to back up the words, but there was not much debate on that. There was not much concern about understanding how full and half page ads differ, for example, or that a magazine has front and back covers.
The debate was on whether any system could understand the sentence well enough to produce an axiom with the semantics “if an ad runs on the back page of the New York Times Magazine it must be a full page ad”.
The only really interesting aspect of this sentence (as far as I was concerned) is the use of “only” as, in effect, a quantifier.
This is no big deal, logically speaking (at least if you don’t limit your thinking to classical first-order logic and allow yourself some generalized quantifiers and relational algebra, both critically important in practice).
The above rendering could be better with regard to “only” but the point is clear enough (assuming functional existentials are intuitive enough); it is logically equivalent to switching the antecedent and consequent of the quantification or the direction of the implication.
(We’ve kept to the simple case here. Another expression of the logic could be rendered as: ∀(?x8)((ad(?x8)∧may(run(on(∃back(page)(of(∃named(New York)(time)(magazine)))))(?x8)))⇒full(page)(color)(?x8)). Essentially, we’ve resolved the scope of the “only” one of several ways.)
In a forthcoming post, we’ll demonstrate the resulting logic in action!
Also, for those interested, the rendered logic is a simplified rendering of a lot of information produced by the natural language processing and linguistic and logical disambiguation processes. Here is another, less simplified rendering FYI:
- ∃(?x11)(∃(?e17)full(?e17)(?x11)∧page(?x11)∧∃(?e5)only(?e5)∧∀(?x8)(∃(?x19)(color(?x19)∧∃(?e12)∃(?e20)compound(?e12)(?x8,?x11)∧compound(?e20)(?x8,?x19)∧ad(?x8))⇒∃(?e3)may((?e3)∃(?x29)(∃(?x35)(back(?x35)∧∃(?x40)(∃(?x46)(named(New York Times)(?x46)∧∃(?e47)compound(?e47)(?x40,?x46)∧magazine(?x40))∧∃(?e34)∃(?e41)compound(?e34)(?x29,?x35)∧page(?x29)∧of(?e41)(?x29,?x40)))∧∃(?e27)∃(?e28)on(?e28)(?e27,?x29)∧run(?e27)(?x8)))))
The more “conflated” rendering is explained in more detail in our patent filings (available on LinkedIn). It is certainly easier on Linguist users and also facilitates more efficient reasoning (including textual entailment, logical implication, and defeasible reasoning).
The representation has further details which relate elements of the logic to the lexicon and the text as well as grammatical and semantic details, such as person, number, gender, tense, aspect, mood, sentence form (e.g., interrogative, declarative, or imperative), etc.